Cho mạch điện \(RLC\) nối tiếp. Cuộn dây không thuần cảm có \(L = \frac{1,4}{\pi}H\) và \(r = 30\Omega\); tụ có \(C = 31,8\mu F\). \(R\) là biến trở. Điện áp hai đầu đoạn mạch có biểu thức: \(u = 100\sqrt2\cos(100\pi t)(V)\). Giá trị nào của \(R\) để công suất trên cuộn dây là cực đại? Giá trị cực đại đó bằng bao nhiêu? Chọn kết quả đúng:
A.\(R = 5\Omega ; P_{cdmax} = 120W.\)
B.\(R = 0\Omega ; P_{cdmax} = 120W.\)
C.\(R = 0\Omega ; P_{cdmax} = 100W.\)
D.\(R = 5\Omega ; P_{cdmax} = 100W.\)

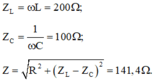
\(Z_L=\omega L=140\Omega\)
\(Z_C=\dfrac{1}{\omega C}=100\Omega\)
Công suất của cuộn dây: \(P_{cd}=I^2.r=\dfrac{U^2}{(R+r)^2+(Z_L-Z_C)^2}.30=\dfrac{100^2}{(R+30)^2+(140-100)^2}.30\)
Từ biểu thức trên ta thấy \(P_{cdmax}\) khi \(R=0\)
Lúc đó \(P_{cdmax}=\dfrac{100^2}{30^2+40^2}.30=120W\)
Chọn đáp án B