Mạch dao động LC lí tưởng, cường độ dòng điện tức thời trong mạch biến thiên theo phương trình \(i = 0,04.\cos \omega t (A)\). Xác định C ? Biết cứ sau những khoảng thời gian nhắn nhất \(0,25 \mu s\) thì năng lượng điện trường và năng lượng từ trường bằng nhau và bằng \(\frac{0,8}{\pi}\mu...
Đọc tiếp
Mạch dao động LC lí tưởng, cường độ dòng điện tức thời trong mạch biến thiên theo phương trình \(i = 0,04.\cos \omega t (A)\). Xác định C ? Biết cứ sau những khoảng thời gian nhắn nhất \(0,25 \mu s\) thì năng lượng điện trường và năng lượng từ trường bằng nhau và bằng \(\frac{0,8}{\pi}\mu J\)
A.\(\frac{125}{\pi}pF.\)
B.\(\frac{100}{\pi}pF.\)
C.\(\frac{120}{\pi}pF.\)
D.\(\frac{25}{\pi}pF.\)
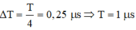
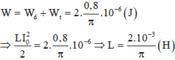
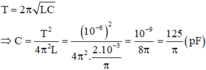
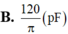
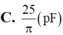
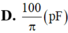
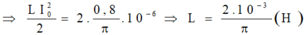
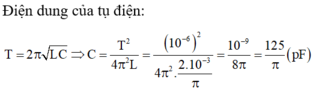
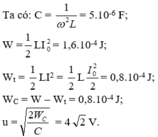
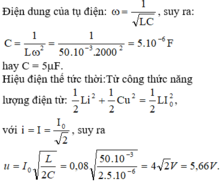
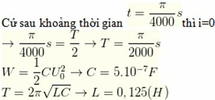
Sau khoảng thời gian ngắn nhất \(0,25 \mu s\) năng lượng điện trường và năng lượng từ trường => \(\frac{T}{4}= 0,25 \mu s=> T = 10^{-6}s=> \omega = \frac{2\pi}{T}= 2\pi.10^{6}(rad/s).\)
\(q_0 = \frac{I_0}{\omega} = \frac{2.10^{-8}}{\pi}C.\)
\(W_L=W_C = \frac{0,8}{\pi}.10^{-6}=> q = \pm \frac{q_0}{\sqrt{2}}.\)
Ta có: \(\frac{1}{2}\frac{q_0^2}{2C}=\frac{0,8}{\pi}.10^{-6}=> C = \frac{1,25.10^{-10}}{\pi}F = \frac{125}{\pi}pF.\)
bạn giải đúng rồi nhưng mà đoạn cuối công thức là (1/2)*(q02/C) chứ ko phải là 2C. đáp án là D