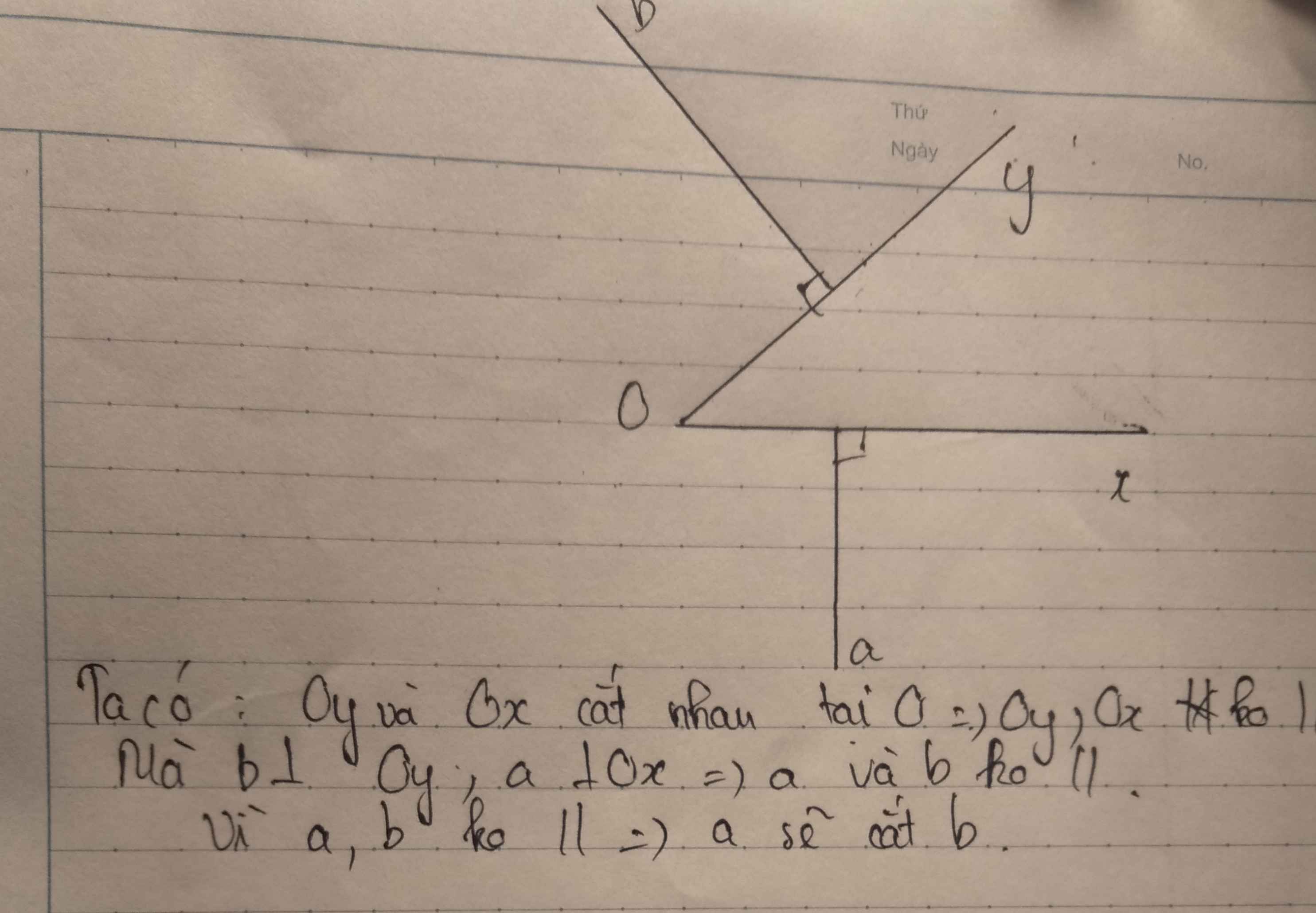
Câu 9:Cho góc xOy, đường thẳng a vuông góc với Ox, đường thẳng b vuông góc với Oy. Hỏi a và b có cắt nhau không? Tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PV
Phạm Vĩnh Linh
27 tháng 7 2021
Đúng(0)
Những câu hỏi liên quan
11 tháng 10 2015
a) +) HE // AK ( cùng vuông góc với Ox) => góc AHE = góc HAK ( So le trong)
+) góc AD // BK (cùng vuông góc với Oy) => HAK + AKB = 180o (2 góc trong cùng phía)
=> góc AHE + AKB = 180o
Theo đề bài : 1/2 AHE = 2/5 AKB nên AHE = 4/5 AKB . thay vào ,ta được: 4/5 AKB + AKB = 180o
=> 9/5.AKB = 180o => AKB = 180o : (9/5) = 100o
=> góc AHE = 180o - 100o = 80o
Vậy....
11 tháng 10 2021
a: Xét ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
\(\widehat{BOF}\) chung
Do đó: ΔOAE=ΔOBF
Suy ra: AE=BF
6 tháng 10 2021
a: Xét ΔOBF vuông tại B và ΔOAE vuông tại A có
OB=OA
\(\widehat{BOF}\) chung
Do đó: ΔOBF=ΔOAE
Suy ra: BF=AE
b: Ta có: ΔOBF=ΔOAE
nên \(\widehat{OFB}=\widehat{OEA}\)
hay \(\widehat{AFI}=\widehat{BEI}\)
7 tháng 3 2022
a: Xét ΔOAN vuông tại A và ΔOBN vuông tại B có
ON chung
\(\widehat{AON}=\widehat{BON}\)
Do đó: ΔOAN=ΔOBN
Suy ra: NA=NB
b: Ta có: ΔOAN=ΔOBN
nên OA=OB
hay ΔOAB cân tại O
c: Xét ΔNAD vuông tại A và ΔNBE vuông tại B có
NA=NB
\(\widehat{AND}=\widehat{BNE}\)
Do đó: ΔNAD=ΔNBE
Suy ra: ND=NE
7 tháng 3 2022
a: Xét ΔOAK vuông tại A và ΔOBK vuông tạiB có
OK chung
\(\widehat{AOK}=\widehat{BOK}\)
Do đó: ΔOAK=ΔOBK
Suy ra: KA=KB
b: Ta có: ΔOAK=ΔOBK
nên OA=OB
hay ΔOAB cân tại O