Đặt điện áp xoay chiều \(u=U_0\cos(100\pi t + \frac {\pi}{3})(V)\) vào hai đầu một cuộn cảm thuần có độ tự cảm \(L=\frac {1}{2\pi} (H)\). Ở thời điểm điện áp giữa hai đầu cuộn cảm là \(100\sqrt2 V\) thì cường độ dòng điện qua cuộn cảm là \(2A\). Biểu thức của cường độ dòng điện qua cuộn cảm là
A.\(i=2\sqrt3 \cos(100\pi t - \frac {\pi}{6})(A).\)
B.\(i=2\sqrt3 \cos(100\pi t + \frac {\pi}{6})(A).\)
C.\(i=2\sqrt2 \cos(100\pi t + \frac {\pi}{6})(A).\)
D.\(i=2\sqrt2 \cos(100\pi t - \frac {\pi}{6})(A).\)

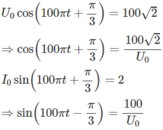

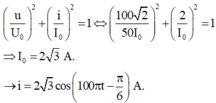
Mạch chỉ có cuôn cảm thì cường độ dòng điện và điện áp tức thời vuông pha tức là
\(\frac{i^2}{I_0^2}+\frac{u^2}{U_0^2} = 1. \)
với \(i = 2A, u = 100\sqrt{2V}\) => \(\frac{4}{I_0^2}+\frac{(100\sqrt{2})^2}{U_0^2} =1\)
mà \(U_0 = I_0 Z_L = 50I_0\)(\(Z_L = L \omega = 50 \Omega.\)) Thay vào phương trình trên ta được
\(\frac{4}{I_0^2}+\frac{20000}{2500.I_0^2} = 1\)=> \(\frac{12}{I_0^2} = 1=> I_0 = 2\sqrt{3}A.\)
Mạch chỉ có cuộn cảm thuần => u sớm pha hơn i là \(\pi/2\). Tức là \(\varphi_u - \varphi_i = \frac{\pi}{2} => \varphi_i = \frac{\pi}{3}-\frac{\pi}{2} = -\frac{\pi}{6}.\)
\(i = 2\sqrt{3} \cos (100\pi t -\frac{\pi}{6})A.\)
Chọn đáp án A bạn nhé.