Một chất điểm dao động điều hòa với chu kì T. Trong khoảng thời gian ngắn nhất khi đi từ vị trí biên có li độ \(x=A\) đến vị trí \(x=\frac{-A} 2\), chất điểm có tốc độ trung bình là:
A.\(\frac{6A} T\)
B.\(\frac{9A}{2T}\)
C.\(\frac {3A}{2T}\)
D.\(\frac {4A} T\)

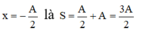
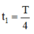
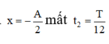
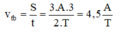
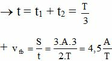

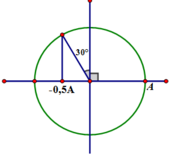
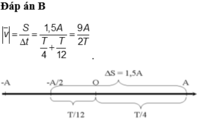
Biểu diễn bằng véc tơ quay ta được:
A -A -A/2 M N O x
Véc tơ quay từ M đến N, khi đó:
+ Góc quay: 90+30 = 1200 =>Thời gian: t = 120/360T = T/3
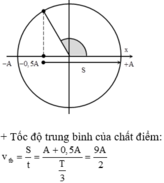
+ Quãng đường dao động: S = A + A/2 = 3A/2
Tốc độ trung bình: \(v_{TB}= \frac{S}{t} = \frac{3A/2}{T/3}=\frac{9A}{2T}\)