Tại hai điểm A và B cách nhau 60cm có hai nguồn sóng kết hợp cùng pha, cùng biên độ 2cm, lamđa 20cm. Coi biên độ không đổi
xác định số điểm dao động với biên độ bằng 3 cm trên đường tròn đường kính AB?
đáp án 24 điểm
mình chưa xem đc lời giải dạng bài này nên giải thử bạn xem giúp mình đúng hay sai nhé.
Giải
A^2=a1^2+a2^2+2a1a2cos (đenta phi)
suy ra 3^2=2^2+2^2+2*2*2cos (đenta phi) suy ra cos (đenta phi)= 1/8
suy ra đenta phi= 0,46pi + k2pi
hoặc đenta phi = -0,46pi+k2pi
ta có đenta phi= phi1 -phi2 + 2pi(d2-d1)/lamđa= 0,1.pi(d2-d1)
TH1: d2-d1=0,46pi + k2pi= 0,1.pi.(d2-d1) suy ra d2-d1= 4,6 + 20k
ép điều kiện d2-d1 suy ra -3,23<k<2,77 ( có 6 gtri k suy ra có 6*2 = 12 điểm trên đường tròn)
TH2: d2-d1=-0,46pi + k2pi = .... (làm tương tự)
suy ra có 6 gtri k suy ra có 12 điểm trên đường tròn.
vậy tổng có 12+12=24 điểm
cái mình hỏi ở đây là chia 2 trường hợp của phi rồi sau đó cộng tổng lại. làm như vậy đúng hay sai hả bạn?

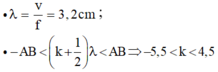
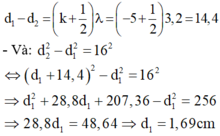
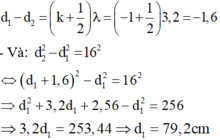
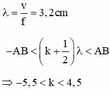
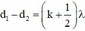
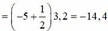

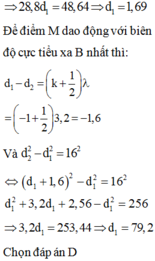





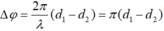
Bạn làm như vậy hoàn toàn đúng rùi.
Đối với bài này ta có thể giải theo phương pháp đếm cho đơn giản.
Ta xét trên đoạn AB, sẽ có những điểm cực đại và cực tiểu xen kẽ nhau, mà mỗi cực đại tương đương như bụng, cực tiểu là nút (giống như sóng dừng).
Số bó sóng: \(\frac{AB}{\frac{\lambda}{2}}=\frac{60}{10}=6\)
Trong mỗi bó sóng sẽ có 2 điểm dao động với biên độ 3cm.
Như vậy, tổng số điểm dao động với biên độ 3cm trên AB là 12 điểm.
Trên cả đường tròn sẽ có tổng: 12.2 = 24 điểm.