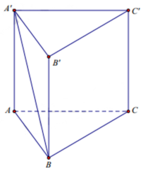
cho hình lăng trụ đứng ABC.A'B'C' có mặt đáy là tam giác ABC vuông tại B và AB=a, BC=2a, AA'=3a. Một mặp phẳng (P) đi qua A và vuông góc với CA' lần lượt cắt các đoạn thẳng CC' và BB' tại M và N.
mọi người giúp mình xác định mặt phẳng (P) với..
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)

ĐÁP ÁN B
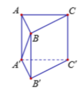
Ta có tan A ' B B ' ⏜ = A ' B ' B B ' = a a 3 = 1 3 ⇒ A ' B B ' ⏜ = 30 °

Chọn D.
Ta có: ![]() nên BB' là hình chiếu của A'B trên (BCC'B')
nên BB' là hình chiếu của A'B trên (BCC'B')
Vậy góc giữa đường thẳng A'B và mặt phẳng (BCC'B') là góc giữa hai đường thẳng A'B và BB' và là góc A ' B B ' ^
Lại có: 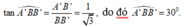

Chọn A
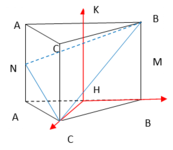
Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
![]()
![]()
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
![]()
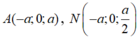
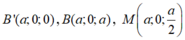
Xét mặt phẳng (BC'N) có
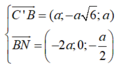
![]()
Phương trình (BC'N) là:
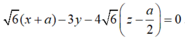
Khoảng cách từ M đến (BC'N) là:
![]()
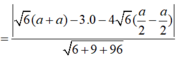


Chọn A.
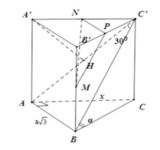
+) Ta có:
![]()
![]()
![]()
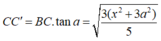
![]()
Ta có:
![]()
![]()
+) Gọi P là trung điểm của B’C’, suy ra:
(MNP)//(ABC')
![]()
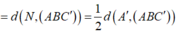
![]()
![]()
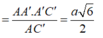
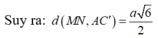
Qua A vẽ đường thẳng vuông góc với CA', cắt CC' tại D.
Nối BA'. Qua A vẽ đường thẳng vuông góc với BA', cắt BB' tại E.
mp (AED) là mặt phẳng P cần tìm.
Bạn tự chứng minh nhé.
ok thanks bạn nhé. mình cũng vẽ kiểu này nhưng không biết chứng minh. giờ chứng minh đc r. :d