Viết 1 số A bất kì có 3 chữ số, viết tiếp 3 chữ số đó 1 lần nữa, được số B có 6 chữ số. Chia số B cho 7, rồi chia thương tìm được cho 11, sau đó lại chia thương tìm được cho 13. Kết quả được số A, hãy giải thích vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2015
Gọi A là abc thì B=abc.1000+abc
Theo đề bài ta có
(abc.1000+abc):7:11:13=abc
abc(1000+1)=abc.1001
abc(1000+1)=abc.1001
Vậy đó mình giải thích xong rồi suy ra B:7:11:13=A
CC
21 tháng 9 2016
Gọi số A là abc. Khi đó số B là abcabc.
Phân tích B=abcabc=abc000+abc=abc.1000+abc=abc.1001=abc.7.11.13.
Bây giờ chia B cho 7,11,13 thì sẽ được A thôi!
BD
21 tháng 9 2016
Viết một số A bất kì có 3 chữ số , viết tiếp 3 chữ số đó một lần nữa , được số B có 6 chữ số . Chia số B cho 7 , rồi chia thương tìm được cho 11 , sau đó lại chia thương tìm được cho 13 . Kết quả được số A , hãy giải thích vì sao ?
Gọi số A là abc. Khi đó số B là abcabc.
Phân tích B=abcabc=abc000+abc=abc.1000+abc=abc.1001=abc.7.11.13.
Bây giờ chia B cho 7,11,13 thì sẽ được A thôi!
8 tháng 6 2016
Số A bất kỳ có 3 chữ số tổng quát là: \(\overline{xyz}\)
Số B là: \(\overline{xyzxyz}=\overline{xyz}\cdot1001=\overline{xyz}\cdot7\cdot11\cdot13\)
Chia B cho 7 được: \(B:7=\overline{xyz}\cdot11\cdot13=B_1\)
Chia thương tìm được B1 cho 11 được: \(B_1:11=\overline{xyz}\cdot13=B_2\)
Chia thương tìm được B2 cho 13 được: \(B_2:13=\overline{xyz}=A\).
8 tháng 6 2016
gọi số A là abc và B là abcabc
B=abcabc=abcx1001
Chia số B cho 7, rồi chia thương tìm được cho 11, sau đó lại chia thương tìm được cho 13:
abcx2001:7:11:13=abc
Do đó được số a.
29 tháng 6 2015
Gọi số a là xyz, ta có b = xyzxyz = xyz . 1001
b / 7 / 11 / 13 = b / 1001 = xyzxyz / 1001 = xyz = a
Hết.
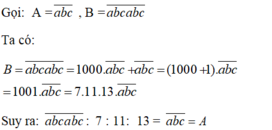
Gọi số A đó là abc
Theo bài ra, ta có:
abcabc:7:11:13 = abc
abcabc:1001 = abc
abcabc = abc.1001
bài toán đc chứng minh