Cho 2 đường thẳng d: y = ax + b và d' : y = a'x + b' (a, a' khác 0)
CMR: nếu d vuông góc với d' thì a.a' = -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Phương trình tổng quát của đường thẳng \(d,d'\) lần lượt là: \(ax - y + b = 0,{\rm{ }}a'x - y + b' = 0\).
Do đó \(\overrightarrow {{n_d}} = \left( {a; - 1} \right),{\rm{ }}\overrightarrow {{n_{d'}}} = \left( {a'; - 1} \right)\).
Ta có \(d \bot d' \Leftrightarrow \overrightarrow {{n_d}} \bot \overrightarrow {{n_{d'}}} \Leftrightarrow \overrightarrow {{n_d}} .\overrightarrow {{n_{d'}}} = 0 \Leftrightarrow a.a' + \left( { - 1} \right)\left( { - 1} \right) = 0 \Leftrightarrow a.a' = - 1\).
CM
8 tháng 6 2019
Đáp án A
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
d cắt d' ⇔ a ≠ a'
CM
12 tháng 1 2017
Đáp án A
Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
d cắt d' ⇔ a ≠ a'
CM
17 tháng 2 2019
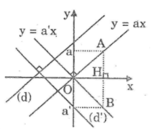
Qua gốc tọa độ, kẻ đường thẳng y = ax // (d) và y = a’x // (d’)
*Chứng minh (d) vuông góc với (d’) thì a.a’ = -1
Không mất tính tổng quát, giả sử a > 0
Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.
Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù (vì các góc tạo bởi đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau 900).
Suy ra: a’ < 0
Mà đường thẳng y = ax đi qua A(1; a), đường thẳng y = a’x đi qua B(1; a’) nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.
Vì (d) ⊥ (d’) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau. Suy ra: góc(AOB) = 90 °
Tam giác vuông AOB có OH ⊥ AB. Theo hệ thức lượng trong tam giác vuông, ta có: OH2 = HA.HB
Hay: a.|a’| = 1 ⇔ a.(-a’) = 1 ⇔ a.a’ = -1
Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1
*Chứng minh a.a’ = -1 thì (d) vuông góc với (d’)
Ta có: a.a’ = -1 ⇔ a.|a’| = 1 hay HA.HB = O H 2
Suy ra OA ⊥ OB hay hai đường thẳng y = ax và y = a’x vuông góc với nhau hay (d) ⊥ (d’)
CM
20 tháng 11 2017
Đáp án A
Cho hai đường thẳng d: y = ax + b(a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
CM
30 tháng 9 2018
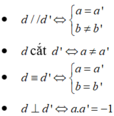
Đáp án A
Cho hai đường thẳng d: y = ax + b(a ≠ 0) và d': y = a'x + b'(a' ≠ 0)
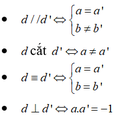
Vì đường thẳng d song song hoặc trùng với đường thẳng d1 : y = ax; đường thẳng d': y = a'x + b' song song hoặc trùng với đường thẳng d2 :
y = a'x nên Nếu d vuông góc với d' thì d1 vuông góc với d2
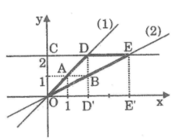
Nhận xét: d1 và d2 đều đi qua gốc O mà d1 vuông góc với d2 nên có 1 đường thẳng nằm trong góc phần tư thứ I và III ( giả sử là d1) ; đường thẳng còn lại nằm trong góc phần tư thứ II và IV . => a > 0 và a' < 0
Lấy H (1; 0). Qua H kẻ đường vuông góc với Ox cắt d1; d2 lần lượt tại B ; A
=> xA = xB = 1
A thuộc d2 => yA = a' ; B thuộc d1 => yB = a
=> HA = |a'|; HB = |a|
Áp dụng hệ thức lượng trong tam giác vuông AOB có: OH2 = HA . HB => 1 = |a|. |a'| => |a.a'| = 1 => a.a' = - 1 ( Vì a;a' trái dấu nên a.a' < 0)
Vậy....