1. Xác định giá trị của tham số m để hs y=x^3 -3mx^2 - m nghịch biến trên khoảng (0;1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có y ' = - 3 x 2 + 6 x + 3 m . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình - 3 x 2 + 6 x + 3 m . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, - 3 x 2 + 6 x + 3 m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
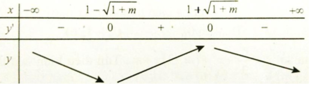
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y ' = - 3 x 2 + 6 x + 3 m ≤ 0 , ∀x > 0 <=> 3 m ≤ 3 x 2 - 6 x , ∀x > 0
Từ đó suy ra 3 m ≤ m i n ( 3 x 2 - 6 x ) với x > 0
Mà 3 x 2 - 6 x = 3 ( x 2 - 2 x + 1 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀ x
Suy ra: m i n ( 3 x 2 – 6 x ) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.

Đáp án: D.
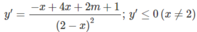
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.

Chọn B.
Tập xác định ![]()
Có 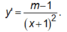
Hàm số nghịch bến trên mỗi khoảng của tập xác định
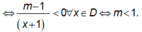

Đáp án: A.
Hàm số nghịch biến trên từng khoảng ( - ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
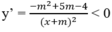
⇔ - m 2 + 5m - 4 < 0
⇔ 

Đáp án: A.
Hàm số nghịch biến trên từng khoảng (- ∞ ; -m), (-m; + ∞ ) khi và chỉ khi
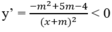
⇔ - m 2 + 5m - 4 < 0
⇔ ![]()
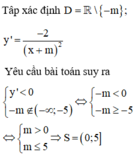
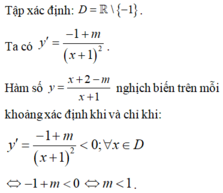
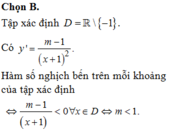
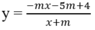
\(y'=3x^2-6mx\)
Hàm nghịch biến trên \(\left(0;1\right)\) khi với mọi \(x\in\left(0;1\right)\) ta có:
\(3x^2-6mx\le0\)
\(\Leftrightarrow3x\left(x-2m\right)\le0\)
\(\Leftrightarrow x-2m\le0\)
\(\Leftrightarrow m\ge\max\limits_{\left(0;1\right)}\dfrac{x}{2}\Rightarrow m\ge\dfrac{1}{2}\)