rút gọn biểu thức
(x + 1) (x2 - x + 1) - (x -1) (x2 + x + 1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


( x 2 + 1 ) ( x − 3 ) − ( x − 3 ) ( x 2 − 1 ) = ( x – 3 ) x 2 + 1 – x 2 – 1 = 2 ( x – 3 )

(x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x)
= (x – 2). [(2x3 – x2 + 1) + x2(1 – 2x)]
= (x – 2). [2x3 – x2 + 1 + x2 . 1 + x2 . (-2x)]
= (x – 2) . (2x3 – x2 + 1 + x2 – 2x3)
= (x – 2) .1
= x – 2

\(a,=\left(x+8-x+2\right)^2=10^2=100\\ b,=x^2\left(x^2-16\right)-\left(x^4-1\right)=x^4-16x^2-x^4+1=1-16x^2\\ c,=x^3+1-x^3+1=2\)

a) Ta có: \(\left(x+2y\right)\left(x^2-2xy+4y^2\right)-\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3+\left(2y\right)^3-\left(x^3-y^3\right)\)
\(=x^3+8y^3-x^3+y^3\)
\(=9y^3\)
b) Ta có: \(\left(x+1\right)\left(x-1\right)^2-\left(x+2\right)\left(x^2-2x+4\right)\)
\(=\left(x+1\right)\left(x^2-2x+1\right)-\left(x+2\right)\left(x^2-2x+4\right)\)
\(=x^3-2x^2+x+x^2-2x+1-\left(x^3+8\right)\)
\(=x^3-x^2-x+1-x^3-8\)
\(=-x^2-x-7\)

1/2 x 2 (6x – 3) – x( x 2 + 1/2) + 1/2.(x + 4)
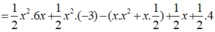
= (3 x 3 – 3/2. x 2 ) – ( x 3 + 1/2.x) + (1/2.x + 2)
= 3 x 3 - 3/2 x 2 – x 3 - 1/2 x + 1/2 x + 2
= ( 3 x 3 – x 3 ) - 3/2. x 2 – (1/2 x - 1/2 x) + 2
= 2 x 3 - 3/2 x 2 + 2
Rút gọn biểu thức:
a) A = x 2 (x - 2) - (x - 1)( x 2 + x + 1);
b) B = ( xy - 1 ) 2 - (xy - 1)(xy + 2).

a) Thực hiện phép nhân và hằng đẳng thức thu được
A = x 3 – 2 x 2 – ( x 3 – 1 3 ); rút gọn A = 1 – 2 x 2 .
b) Đặt (xy – 1) làm nhân tử chung ta được B = 3(1 – xy).

\(A=x^2+4x-21-x^2-4x+5=-16\\ B=-2\left(4x^2+20x+25\right)-\left(1-16x^2\right)\\ B=-8x^2-40x-50-1+16x^2=8x^2-40x-51\\ C=x^2\left(x^2-16\right)-\left(x^4-1\right)=x^4-16x^2-x^4+1=1-16x^2\\ D=x^3+1-\left(x^3-1\right)=2\\ E=x^3-3x^2+3x-1-x^3+1-9x^2+1=-12x^2+3x+1\)
(x + 1) (x2 - x + 1) - (x -1) (x2 + x + 1)
= x3 + 1 - (x3 - 1) ( áp dụng hằng đẳng thức số 6 và 7 )
= x3 + 1 - x3 + 1
= 2