Cho \(\widehat{xoy}\) = 100o. Vẽ tia Oz là tia đối cua rtia Ox.Gọi Ot là tia phân giác của \(\widehat{yoz}\). Tính \(\widehat{yot}\), \(\widehat{xot}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

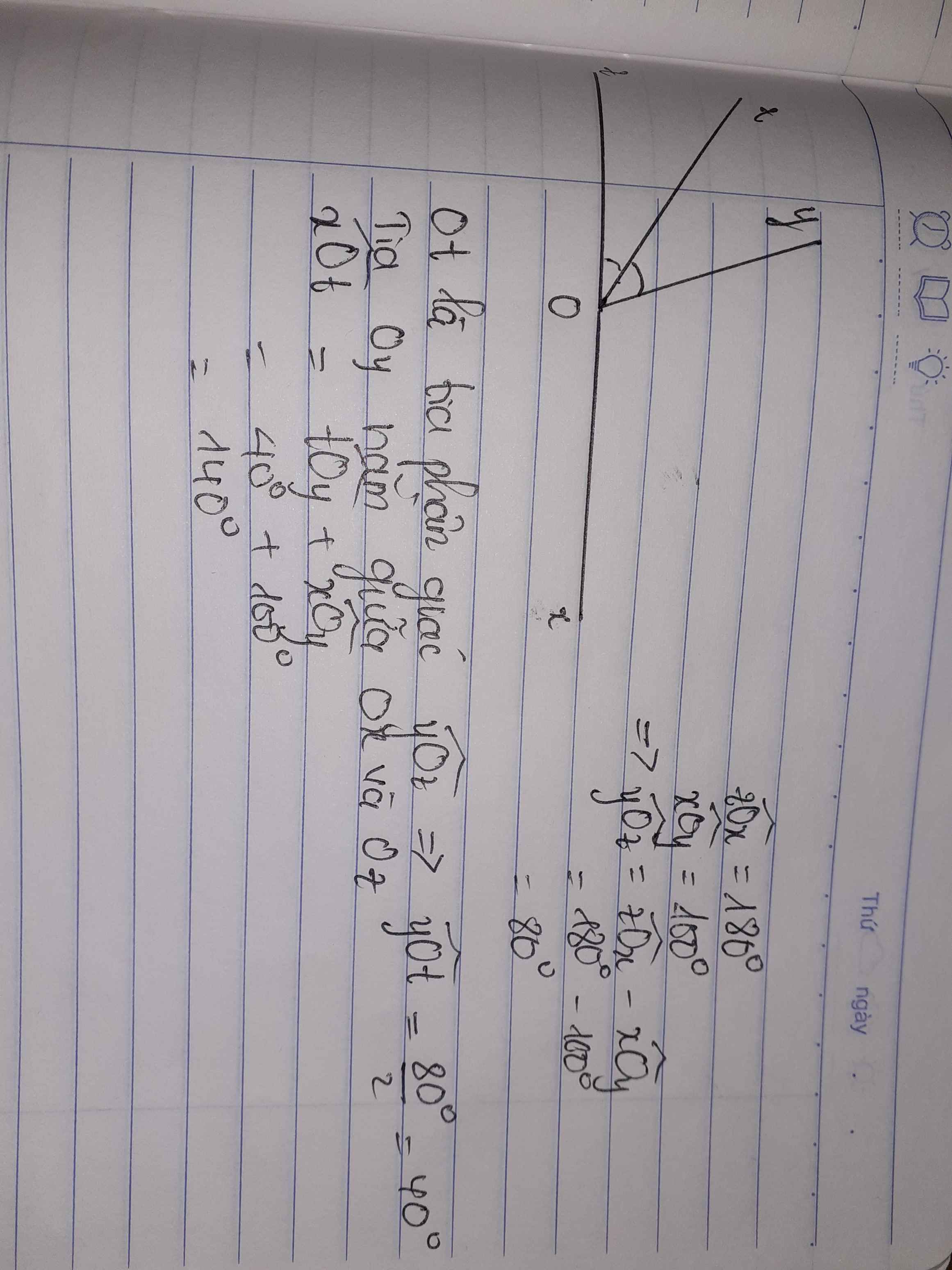

Bạn tự vẽ hình nhé!
a. Vì \(\widehat{xOt}>\widehat{xOy}\)
=> Ot nằm giữa 2 tia Ox và Oy
Ta có:\(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)
Thay:\(\widehat{xOt}=120^o,\)\(\widehat{xOy}=180^0\)
=>\(\widehat{yOt}=180^0-120^0\)
Vậy:\(\widehat{yOt}=60^0\)
b. \(\widehat{yOz}=\widehat{xOy}:2\)
Thay:\(\widehat{xOy}=180^0\)
=>\(\widehat{yOx}=180^0:2\)
Vậy:\(\widehat{yOx}=90^0\)
\(\widehat{zOt}=\widehat{xOt}-\widehat{xOz}\)
Thay:\(\widehat{xOt}=120^0,\widehat{xOz}=90^0\)
=>\(\widehat{zOt}=120^0-90^0\)
Vậy:\(\widehat{xOt}=30^0\)
c. Mình thấy đề hơi sai sai thì phải, góc xOy= 180^0 mà Om là tia đối của Ox thì chẳng lẽ Om là Oy hả?

a) Ta có: \(\widehat{xOm}+\widehat{yOm}=180^0\)(Hai góc kề bù)
\(\Leftrightarrow\widehat{yOm}+30^0=180^0\)
hay \(\widehat{yOm}=150^0\)
Vậy: \(\widehat{yOm}=150^0\)
b) Ta có: tia Ot là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{yOt}=\widehat{xOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}\)
hay \(\widehat{yOt}=90^0\)(đpcm)

a)
vì \(\widehat{xoy}< \widehat{xoz}\left(30^o< 100^o\right)\) nên tia Oy nằm giữ 2 tia Ox và Oz, ta có :
\(\widehat{xoz}=\widehat{xoy}+\widehat{yoz}\)
\(\Rightarrow\widehat{yoz}=\widehat{xoz}-\widehat{xoy}=100^o-30^o=70^o\)
vậy \(\widehat{yoz}=70^o\)
b)
ta có tia ot nằm giữa 2 tia Oy và Oz nên ta có :
\(\widehat{yoz}=\widehat{yot}+\widehat{toz}\)
\(\Rightarrow\widehat{toz}=\widehat{yoz}-\widehat{yot}=70^o-20^o=50^o\)
ta có Ot nằm giữa 2 tia Oy và Oz
vì \(\widehat{toz}=50^o\) nên \(\widehat{toz}\ne\widehat{yot}\left(50^o\ne70^o\right)\) ⇒ tia ot không phải là phân giác của \(\widehat{yoz}\)
c)
ta có tia Ot nằm giữa 2 tia Ox và Oz nên
\(\widehat{xoz}=\widehat{xot}+\widehat{toz}\)
\(\Rightarrow\widehat{xot}=\widehat{xoz}-\widehat{toz}=100^o-50^o=50^o\)
vì tia Ot nằm giữa 2 tia Ox và Oz
và \(\widehat{xot}=\widehat{toz}\left(=50^o\right)\) nên tia Ot là phân giác của \(\widehat{xoz}\)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{yOz}+30^0=100^0\)
hay \(\widehat{yOz}=70^0\)
Vậy: \(\widehat{yOz}=70^0\)

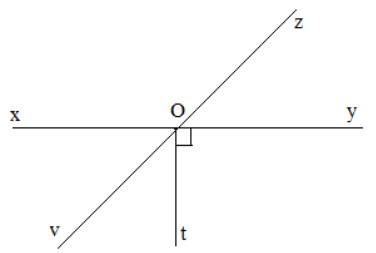
Vì \(\widehat {yOt} = 90^\circ \Rightarrow Oy \bot Ot \Rightarrow Ox \bot Ot\) nên \(\widehat {xOt} = 90^\circ \)
Vì Ov là tia phân giác của \(\widehat {xOt}\) nên \(\widehat {xOv} = \widehat {vOt} = \frac{1}{2}.\widehat {xOt} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {vOz} =\widehat {vOx} + \widehat {xOz} = 45^\circ + 135^\circ = 180^\circ \) nên Ov và Oz là hai tia đối nhau
Như vậy, các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz

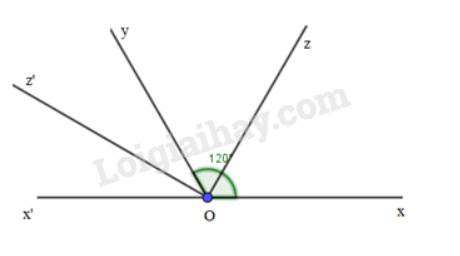
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau