Trên đường thẳng AB lấy điểm O. Vẽ tia OC sao cho AOC-COB=40 độ
a) Tính số đo các góc AOC, COB
b) Vẽ tia OD nằm giữa các tia OA, OC sao cho AOD=40 độ. Chứng tỏ rằng tia OD là tia phân giác của góc BOD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

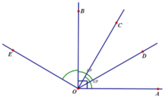
a: Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOb}< \widehat{aOc}\)
nên tia Ob nằm giữa hai tia Oa và Oc
Suy ra: \(\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
hay \(\widehat{bOc}=70^0\)

a) Vì tia OD nằm trong A O B ^ nên tia OD nằm giữa hai tia OA và OB do đó
A O D ^ + B O D ^ = A O B ^
Suy ra: A O D ^ = A O B ^ − B O D ^ = 90 0 − 60 0 = 30 0
Tương tự ta cũng có C O B ^ = 30 0 , D O C ^ = 30 0 .
b) Vì là tia phân giác của D O E ^ nên D O B ^ = B O E ^ = 60 0 .
Vì OB nằm giữa hai tia OC và OE và C O B ^ = 30 0 nên ta có
E O C ^ = E O B ^ + B O C ^ = 60 0 + 30 0 = 90 0
Vậy O C ⊥ O E

Bài 2: ta có: góc AOC+góc AOD=180 độ(vì kề bù) mà góc AOC-AOD= 20 độ => AOC= (180+20):2= 100độ
=> AOD= 100- 20= 80độ
ta có: COB = AOD( vì đối đỉnh)=> COB=80độ
BOD=AOC (vì đối đỉnh)=> BOD=100độ

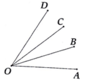
a) Ta có A O B ^ < A O C ^ nên tia OB nằm giữa hai tia OA và OC. Theo tính chất cộng góc, suy ra 20°, nên A O B ^ = B O C ^ . Vậy OB là tia phân giác của góc AOC.
b) Tương tự ý a), tính được
C O D ^ = 20° và B O D ^ = 40°.
c) Ta có B O C ^ = C O D ^ = B O D ^ 2 (cùng bằng 20°). Do đó, tia OC là tia phân giác của góc BOD.
a)ta co : goc AOC - COB=40--> goc AOC =40+ goc COB
ma AOC+COB =180 ( 2 goc ke bu)
nen goc 40+ goc COB+ goc COB=180
-_> 2 goc COB=180-40=140
--> goc COB =140:2=70
--> goc AOC =70+40=110
b)Vi tia OD nam giua hai tia OA va OC nen ta co : goc AOD + goc DOC = goc AOC
--> 40+ goc DOC=110-> goc DOC=110-40=70
ta co : gpc DOC =70 va goc BOC =70 ---> goc DOC= goc BOC
ta co : tia OC nam giua hai tia OB va OA
tia OD nam giua hai tia OC va OA
===> tia OC nằm giữa hai tia OB và OD
ta co : tia OC nam giua hai tia OB va OD
goc DOC = goc BOC
--> tia OC la tia phan giac goc BOD