Cho 4 điểm A, B, C, D không đồng phẳng. Gọi M, N lần lượt là trung điểm của AB, AD. P là điểm trên đoạn AC sao cho PA=2PC. Tìm giao tuyến của (MP) và (BCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 7 2017
Đáp án A
D ∈ AM ⇒ D ∈ (AMN)
N ∈ BC ⇒ N ∈ (BCD)
Xét (AMN) và (BCD) có:
D là điểm chung
N là điểm chung
⇒ Giao tuyến của 2 mặt phẳng là ND
CM
16 tháng 9 2019
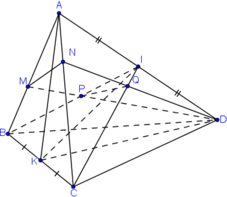
a) Tìm giao tuyến của mp(IBC) và mp(KAD).
Ta có:
K ∈ BC ⇒ K ∈ (IBC) ⇒ K ∈ (IBC) ∩ (KAD)
I ∈ AD ⇒ I ∈ (KAD) ⇒ I ∈ (IBC) ∩ (KAD)
Vậy KI = (IBC) ∩ (KAD)
b) Trong mp(ABD) gọi BI ∩ DM = P
⇒ P ∈ (IBC) ∩ (DMN)
Trong mặt phẳng (ACD) gọi CI ∩ DN = Q
⇒ Q ∈ (IBC) ∩ (DMN)
Vậy (IBC) ∩ (DMN) = PQ.
Q
31 tháng 3 2017
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm.
BT
6 tháng 6 2017
a) \(I\in AD\) nên \(I\in\left(IBC\right)\cap\left(KAD\right)\);
\(K\in BC\) nên \(K\in\left(IBC\right)\cap\left(KAD\right)\).
Vì vậy: \(IK\in\left(IBC\right)\cap\left(KAD\right)\).
b)
Gọi \(P=CI\cap DN\) . Do \(\left\{{}\begin{matrix}P\in CI\\P\in DN\end{matrix}\right.\) nên \(P\in\left(IBC\right)\cap\left(DMN\right)\).
Gọi \(Q=BI\cap MD\). Do \(\left\{{}\begin{matrix}Q\in BI\\Q\in MD\end{matrix}\right.\) nên \(Q\in\left(IBC\right)\cap\left(DMN\right)\).
Vậy PQ là giao tuyến của (IBC) và (DMN).
CM
11 tháng 4 2019
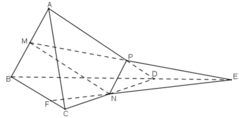
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.
CM
24 tháng 5 2019
Đáp án D
M ∈ AD ⇒ M ∈ (NDA)
N ∈ BC N ∈ ( MBC)
Xét (NDA) và (MBC) có
M là điểm chung
N là điểm chung
⇒ Giao tuyến của 2 mặt phẳng là MN
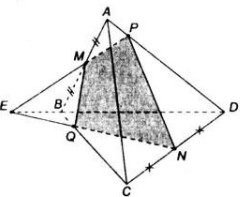
Trong mp (ABC), nối MP kéo dài cắt BC kéo dài tại E
Trong mp (ACD), nối NP kéo dài cắt CD kéo dài tại F
\(\Rightarrow EF=\left(MNP\right)\cap\left(BCD\right)\)