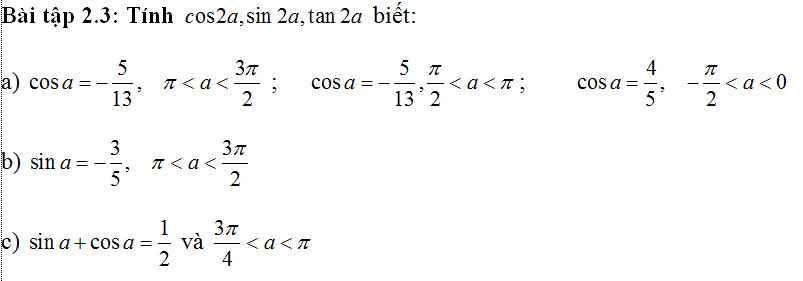
định hướng cách làm giúp mk vs ạ thank nhiều!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Ta thấy: $-1\leq \cos x\leq 1$
$\Leftrightarrow 1\leq 2\cos x+3\leq 5$
$\Leftrightarrow 1\leq \sqrt{2\cos x+3}\leq \sqrt{5}$
$\Leftrightarrow -3\leq \sqrt{2\cos x+3}-4\leq \sqrt{5}-4$
Vậy $y_{\min}=-3$ khi $x=(2k+1)\pi$, $y_{\max}=\sqrt{5}-4$ khi $x=2k\pi$ với $k$ nguyên.
2.
\(y=\cos ^2x-6\sin x+3=1-\sin ^2x-6\sin x+3\)
\(=-\sin ^2x-6\sin x+4\)
Ta thấy: $\sin ^2x\leq 1\Rightarrow -\sin ^2x\geq -1$
$\sin x\leq 1\Leftrightarrow -6\sin x\geq -6$
$\Rightarrow y=-\sin ^2x-6\sin x+4\geq -1-6+4=-3$
Vậy $y_{\min}=-3$. Giá trị này đạt tại $x=2k\pi +\frac{\pi}{2}$ với $k$ nguyên.
Mặt khác:
\(y=-\sin ^2x-6\sin x+4=9-(\sin x+1)(\sin x+5)\)
$-1\leq \sin x\leq 1\Rightarrow (\sin x+1)(\sin x+5)\geq 0$
$\Rightarrow y=9-(\sin x+1)(\sin x+5)\leq 9$
Vậy $y_{\max}=9$. Giá trị này đạt tại $x=2k\pi -\frac{\pi}{2}$ với $k$ nguyên.

nSO2=0,1(mol); nO2=0,1(mol)
a) PTHH: 2 SO2 + O2 \(⇌\) 2 SO3 (xt: V2O5)
Ta có: 0,1/2 < 0,1/1
=> O2 dư, SO2 hết, tính theo nSO2.
b) nSO3=nSO2=0,1(mol)
=> mSO3=0,1.80=8(g)

câu 8:
thời gian người đó đi từ A đến B:
\(t=8h5'-7h20'=45'=\dfrac{3}{4}h\)
vận tốc của người đó \(V=\dfrac{S}{t}=\dfrac{24,3}{\dfrac{3}{4}}=32,4km/h=9m/s\)
caau9: đổi \(5m/s=18km/h\)
gọi thời gian người đi xe đạp đi là : \(t\left(h\right)\)
thời gian người đi xe máy: \(t-2\left(h\right)\)
quãng đường người đi xe đạp đi tới khi gặp xe máy:
\(S1=18t\left(km\right)\)
Quãng đường người đi xe máy đi tới khi gặp xe đạp:
\(S2=36\left(t-2\right)\left(km\right)\)
mà \(S1=S2=>18t=36\left(t-2\right)=>t=4\)
vậy 2 người gặp nhau lúc \(8+4=12h\)
nơi gặp nhau cách A là \(S1=18.4=72km\)




a) Thay m=3 vào hệ pt, ta được:
\(\left\{{}\begin{matrix}x+3y=3\\3x+4y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+9y=9\\3x+4y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=3\\x+3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{3}{5}\\x=3-3y=3-3\cdot\dfrac{3}{5}=\dfrac{6}{5}\end{matrix}\right.\)
Vậy: Khi m=3 thì hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(\dfrac{6}{5};\dfrac{3}{5}\right)\)
a.
\(\pi< a< \dfrac{3\pi}{2}\Rightarrow sina< 0\)
\(\Rightarrow sina=-\sqrt{1-cos^2a}=-\dfrac{12}{13}\)
\(cos2a=cos^2a-sin^2a=\left(-\dfrac{5}{12}\right)^2-\left(-\dfrac{12}{13}\right)^2=...\)
\(sin2a=2sina.cosa=...\)
\(tan2a=\dfrac{sin2a}{cos2a}=...\)
//
\(\dfrac{\pi}{2}< a< \pi\Rightarrow sina>0\Rightarrow sina=\sqrt{1-cos^2a}=\dfrac{12}{13}\)
\(cos2a=cos^2a-sin^2a=...\) ; \(sin2a=2sina.cosa\) ; \(tan2a=\dfrac{sin2a}{cos2a}\) ...
//
\(-\dfrac{\pi}{2}< a< 0\Rightarrow sina< 0\Rightarrow sina=-\sqrt{1-cos^2a}=-\dfrac{3}{5}\)
Thay vào tính cos2a, sin2a, tan2a tương tự như trên
b.
\(\pi< a< \dfrac{3\pi}{2}\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
Tính tương tự câu a
c.
\(\dfrac{3\pi}{4}< a< \pi\Rightarrow\dfrac{3\pi}{2}< 2a< 2\pi\Rightarrow cos2a>0\)
\(sina+cosa=\dfrac{1}{2}\Rightarrow\left(sina+cosa\right)^2=\dfrac{1}{4}\)
\(\Rightarrow1+2sina.cosa=\dfrac{1}{4}\Rightarrow1+sin2a=\dfrac{1}{4}\)
\(\Rightarrow sin2a=-\dfrac{3}{4}\)
\(cos2a=\sqrt{1-sin^22a}=\dfrac{\sqrt{7}}{4}\)
\(tan2a=\dfrac{sin2a}{cos2a}=...\)