giải pt:
a) (x2-3x)(x2+7x+10)=216
b) (2x2-7x+3)(2x2+x-3)+9=0
c) (4x+3)2(2x+1)(x+1)=72
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(x^2-3x\right)\left(x^2+7x+10\right)=216\Rightarrow x\left(x-3\right)\left(x+2\right)\left(x+5\right)=216\)
\(\Rightarrow x\left(x+2\right)\left(x-3\right)\left(x+5\right)=216\Rightarrow\left(x^2+2x\right)\left(x^2+2x-15\right)=216\)
Đặt \(t=x^2+2x\Rightarrow\) pt trở thành \(t\left(t-15\right)=216\Rightarrow t^2-15t-216=0\)
\(\Rightarrow\left(t+9\right)\left(t-24\right)=0\Rightarrow\left[{}\begin{matrix}t=-9\\t=24\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x^2+2x=-9\\x^2+2x=24\end{matrix}\right.\)
\(TH_1:x^2+2x=-9\Rightarrow x^2+2x+9=0\Rightarrow\left(x+1\right)^2+8=0\) (vô lý)
\(TH_2:x^2+2x=24\Rightarrow x^2+2x-24=0\Rightarrow\left(x-4\right)\left(x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-6\end{matrix}\right.\)
b) \(\left(2x^2-7x+3\right)\left(2x^2+x-3\right)+9=0\)
\(\Rightarrow\left(x-3\right)\left(2x-1\right)\left(x-1\right)\left(2x+3\right)+9=0\)
\(\Rightarrow\left(x-3\right)\left(2x+3\right)\left(x-1\right)\left(2x-1\right)+9=0\)
\(\Rightarrow\left(2x^2-3x-9\right)\left(2x^2-3x+1\right)+9=0\)
Đặt \(t=2x^2-3x-9\Rightarrow\) pt trở thành \(t\left(t+10\right)+9=0\)
\(\Rightarrow t^2+10t+9=0\Rightarrow\left(t+1\right)\left(t+9\right)=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-9\end{matrix}\right.\)
\(TH_1:t=-1\Rightarrow2x^2-3x-9=-1\Rightarrow2x^2-3x-8=0\)
\(\Delta=\left(-3\right)^2-4\left(-8\right).2=73\Rightarrow\left[{}\begin{matrix}x=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-\sqrt{73}}{4}\\x=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+\sqrt{73}}{4}\end{matrix}\right.\)
\(TH_2:t=-9\Rightarrow2x^2-3x-9=-9\Rightarrow2x^2-3x=0\Rightarrow x\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)

a: \(=6x^3-10x^2+6x\)
b: \(=-2x^4-10x^3+6x^2\)
c: \(=-x^5+2x^3-\dfrac{3}{2}x^2\)
d: \(=2x^3+10x^2-8x-x^2-5x+4=2x^3+9x^2-13x+4\)

\(a,\Leftrightarrow\left(2x-3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow x^3-27-x^3+4x=1\\ \Leftrightarrow4x=28\Leftrightarrow x=7\\ c,\Leftrightarrow4x^2-4x-8=0\\ \Leftrightarrow x^2-x-2=0\\ \Leftrightarrow\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ d,\Leftrightarrow2x^2+6x+x+3=0\\ \Leftrightarrow\left(x+3\right)\left(2x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{1}{2}\end{matrix}\right.\)

`@` `\text {Ans}`
`\downarrow`
`1.`
\(\left(-4xy\right)\cdot\left(2xy^2-3x^2y\right)\)
`=`\(\left(-4xy\right)\left(2xy^2\right)+\left(-4xy\right)\left(-3x^2y\right)\)
`=`\(-8\left(x\cdot x\right)\left(y\cdot y^2\right)+12\left(x\cdot x^2\right)\left(y\cdot y\right)\)
`=`\(-8x^2y^3+12x^3y^2\)
`2.`
\(\left(-5x\right)\left(3x^3+7x^2-x\right)\)
`=`\(\left(-5x\right)\left(3x^3\right)+\left(-5x\right)\left(7x^2\right)+\left(-5x\right)\left(-x\right)\)
`=`\(-15x^4-35x^3+5x^2\)
`3.`
\(\left(3x-2\right)\left(4x+5\right)-6x\left(2x-1\right)\)
`=`\(3x\left(4x+5\right)-2\left(4x+5\right)-12x^2+6x\)
`=`\(12x^2+15x-8x-10-12x^2+6x\)
`=`\(\left(12x^2-12x^2\right)+\left(15x-8x+6x\right)-10\)
`=`\(13x-10\)
`4.`
\(2x^2\left(x^2-7x+9\right)\)
`=`\(2x^2\cdot x^2+2x^2\cdot\left(-7x\right)+2x^2\cdot9\)
`=`\(2x^4-14x^3+18x^2\)
`5.`
\(\left(3x-5\right)\left(x^2-5x+7\right)\)
`=`\(3x\left(x^2-5x+7\right)-5\left(x^2-5x+7\right)\)
`=`\(3x^3-15x^2+21x-5x^2+25x-35\)
`=`\(3x^3-20x^2+46x-35\)

a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
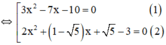
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
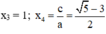
Vậy phương trình có tập nghiệm 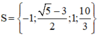
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
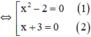
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
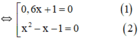
+ Giải (1): 0,6x + 1 = 0 ⇔ 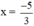
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 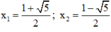
Vậy phương trình có tập nghiệm 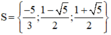
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
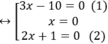
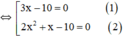
+ Giải (1): 3x – 10 = 0 ⇔ 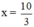
+ Giải (2):
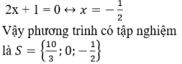

Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4

Dễ
Thế
Mà
Cũnhoir
Dc
Ạ
Chịu
Chắc
Phải
Ngu
Lamqs
Mới
Hỏi
Câu
Này
a) ( x2 - 3x )( x2 + 7x + 10 ) = 216
<=> x( x - 3 )( x + 2 )( x + 5 ) - 216 = 0
<=> [ x( x + 2 ) ][ ( x - 3 )( x + 5 ) ] - 216 = 0
<=> ( x2 + 2x )( x2 + 2x - 15 ) - 216 = 0 (1)
Đặt a = x2 + 2x
(1) trở thành a( a - 15 ) - 216 = 0 <=> a2 - 15a - 216 = 0 <=> ( a - 24 )( a + 9 ) = 0 <=> a = 24 hoặc a = -9
=> \(\orbr{\begin{cases}x^2+2x=24\\x^2+2x=-9\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2+2x-24=0\\x^2+2x+9=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(x-4\right)\left(x+6\right)=0\\\left(x+1\right)^2+8>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-6\end{cases}}\)
Vậy S = { 4 ; -6 }
b) ( 2x2 - 7x + 3 )( 2x2 + x - 3 ) + 9 = 0
<=> ( x - 3 )( 2x - 1 )( x - 1 )( 2x + 3 ) + 9 = 0
<=> [ ( x - 3 )( 2x + 3 ) ][ ( 2x - 1 )( x - 1 ) ] + 9 = 0
<=> ( 2x2 - 3x - 9 )( 2x2 - 3x + 1 ) + 9 = 0
<=> ( 2x2 - 3x - 4 - 5 )( 2x2 - 3x - 4 + 5 ) + 9 = 0
<=> ( 2x2 - 3x - 4 )2 - 16 = 0
<=> x( 2x - 3 )( 2x2 - 3x - 8 ) = 0
<=> x = 0 hoặc 2x - 3 = 0 hoặc 2x2 - 3x - 8 = 0
<=> x = 0 hoặc x = 3/2 hoặc x = \(\frac{3\pm\sqrt{73}}{4}\)
Vậy S = { 0 ; 3/2 ; \(\frac{3\pm\sqrt{73}}{4}\)}