cho tam giác ABC M là trung điểm của cạnh AB , N là trung điểm của cạnh BC Chứng tỏ các đoạn MN, NP và BM chia tam giác ABC thành 4 phần có diện tích bằng nhau
B biết rằng AB , BN và CM cắt nhau tại điểm O chứng ỏ rằng OA gấp đôi đoạn OB
C Gọi I là một điểm nằm trên BC và đoạn BI gấp 3 lần đoạn IC người ta kéo dài đoạn IC người ta kéo dài đoạn ơi một đoạn bằng đoạn NY 1 doạn NY IK bằng đoạn NI gọi tam giác ABC là a Hãy tính diện tích tam giác bnk theo a


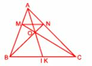
a) Xét ΔMAN và ΔDCN:
AN=NC(GT)
ANM=CNM(đối đỉnh)
MN=ND(GT)
->ΔMAN=ΔDCN(c.g.c)(1)
->AM=CD,(tương ứng)
mà AM=MB(GT)
->MB=CD(đpcm)
Từ(1)->góc A=góc ACN.Mà 2 góc ở vị trí đồng vị->AM//CD
->BM//CD(đpcm)
bạn lớp mấy đây