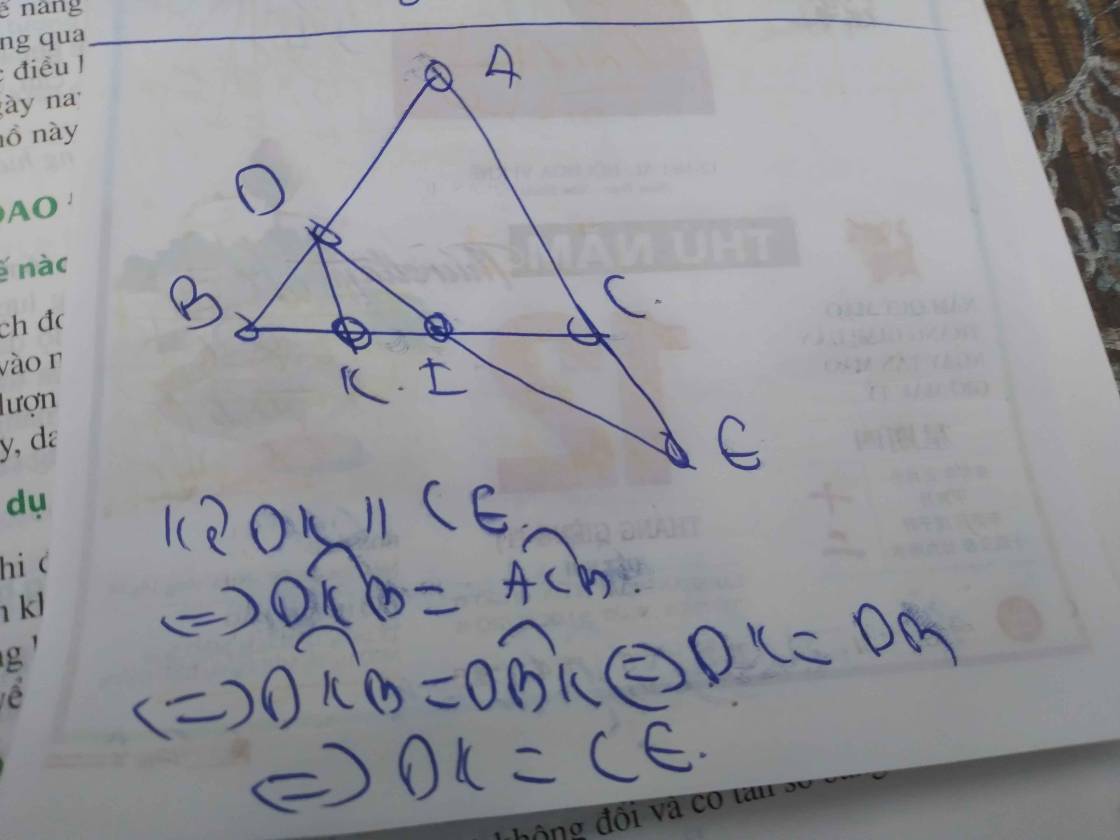
Cho tam giác ABC,AB=AC.Lấy điểm D trên cạnh AD,điểm E thuộc tia đối của tia đối của tia CA.Sao cho BD=CE.Gọi I là giao điểm của DE với BC.Chứng minh DI=IE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2017
Qua D kẻ DH// BC( H thuộcAC)
xét tg DHCB có: DH//BC( cách vẽ) và DBC=HCB (vì tg ABC cân tại A)=> tg DHCB là hthang cân=> DB=HC
xét tg DHE có: HC=CE(= BD) va DH//FC( vì DH//BC, F thuộc BC)=> F là t/đ của DE
Nếu đúng xin háy k cho mk nha!
6 tháng 8 2017
Vẽ DG // BC và cắt AC tại G
Do DG // BC nên tứ giác DGCB là hình thang ( đáy DG // BC), mà tam giác ABC cân tại A => góc B = C => DGBC là hình thang cân ( đáy DG // BC) => DB = GC ( tính chất của hình thang cân)
Mà DB = CE => GC = CE và C thuộc GE => C là tđ của GE
Xét tam giác DGE có: C là tđ GE ; CF // DG ( Do DG // BC mà CF thuộc BC) => CF là đg trung bình ứng vs đáy DG của tam giác DGE => F là trung điểm của DE
NOTE : cái này mik làm đại, nghĩ sao làm vậy, ko bik đúng hay sai, nếu sai thì đừng trách mik
4 tháng 2 2017
Từ D kẻ DI // AE
Vì \(\Delta\)ABC cân tại A nên \(\widehat{B}\) = \(\widehat{ACB}\) (1)
Vì DI // AE => \(\widehat{ACB}\) = \(\widehat{DIB}\) (đồng vị ) (2)
Từ (1) và (2) => \(\widehat{B}\) = \(\widehat{DIB}\)
Trong \(\Delta\)DIB có : \(\widehat{B}\) = \(\widehat{DIB}\) => \(\Delta\)DIB cân tại D
=> DB = DI mà DB = CE (gt)
=> DI = CE
Vì DI // AE => \(\widehat{MDI}\) = \(\widehat{MEC}\)(so le trong )
và \(\widehat{DIM}\) = \(\widehat{MCE}\) ( so le trong )
Xét \(\Delta\)DIM và \(\Delta\)ECM có :
\(\widehat{MDI}\) = \(\widehat{MEC}\) (chứng minh trên )
DI = CE (chứng minh trên ) \(\widehat{DIM}\) = \(\widehat{MCE}\)(chứng minh trên ) => \(\Delta\)DIM = \(\Delta\)ECM (g-c-g) => DM = ME ( cặp cạnh tương ứng ) => ĐPCM
4 tháng 1 2022
Ta có: AB+BD=AD
AC+CE=AE
mà AB=AC
và BD=CE
nên AD=AE
Xét ΔCDE và ΔBED có
CE=BD
\(\widehat{CED}=\widehat{BDE}\)
DE chung
Do đó: ΔCDE=ΔBED
Suy ra: \(\widehat{IDE}=\widehat{IED}\)
hay ΔIDE cân tại I
Xét ΔACD và ΔABE có
AC=AB
\(\widehat{A}\) chung
AD=AE
Do đó: ΔACD=ΔABE
Suy ra: CD=BE
Ta có: BI+IE=BE
CI+ID=CD
mà BE=CD
và ID=IE
nên BI=CI