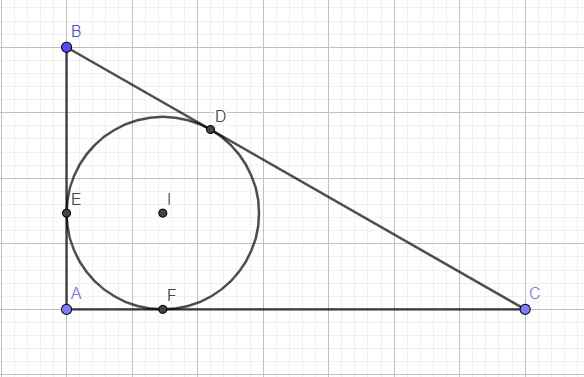
Cho đường tròn nội tiếp \(\Delta\)ABC tiếp xúc 3 cạnh AB; BC; AC tại các điểm D, E, F. Đường thẳng qua D song song với BC cắt EF tại G. Chứng minh rằng trung điểm I của DG nằm trên AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)

Bổ sung: ΔABC cân tại A
ΔABC cân tại A
=>AO đi qua trug diểm I của EF
Vẽ IK vuông góc AB tại K, gọi H và G lần lượt là giao của OA với BC và(O)
Vì OE vuông góc AB, IK vuông goc AB, GB vuông góc AB
=>OE//IK//GB
ΔABG có IK//GB
nên IK/BG=AI/AG
=>IK=AI*BG/AG
ΔABH có EI//BH
ΔABE có OE//BG
=>IH/AH=BE/BA=OG/AG và AE/AB=AI/AH
=>IH=AH*OE/AE
ΔABG có OE//BG
nên AB/AE=BG/OE
AH/AI=AB/AE=BG/OE
=>AH*OE=AI*BG
=>AH*OG=AI*BG
=>IK=IH
=>ĐPCM

Ta có: AE’ = AF’, BD’ = BF’, CD’ = CE’ (tính chất hai tiếp tuyến cắt nhau).
Suy ra
AE’ + AF’ = (AC + CE’) + (AB + BF’)
= (AC + CD’) + (AB + BD’) = AC + BC + AB = 2p.
Do đó: AE’ = AF’ = p.