Mn giúp em bài 2 với ạ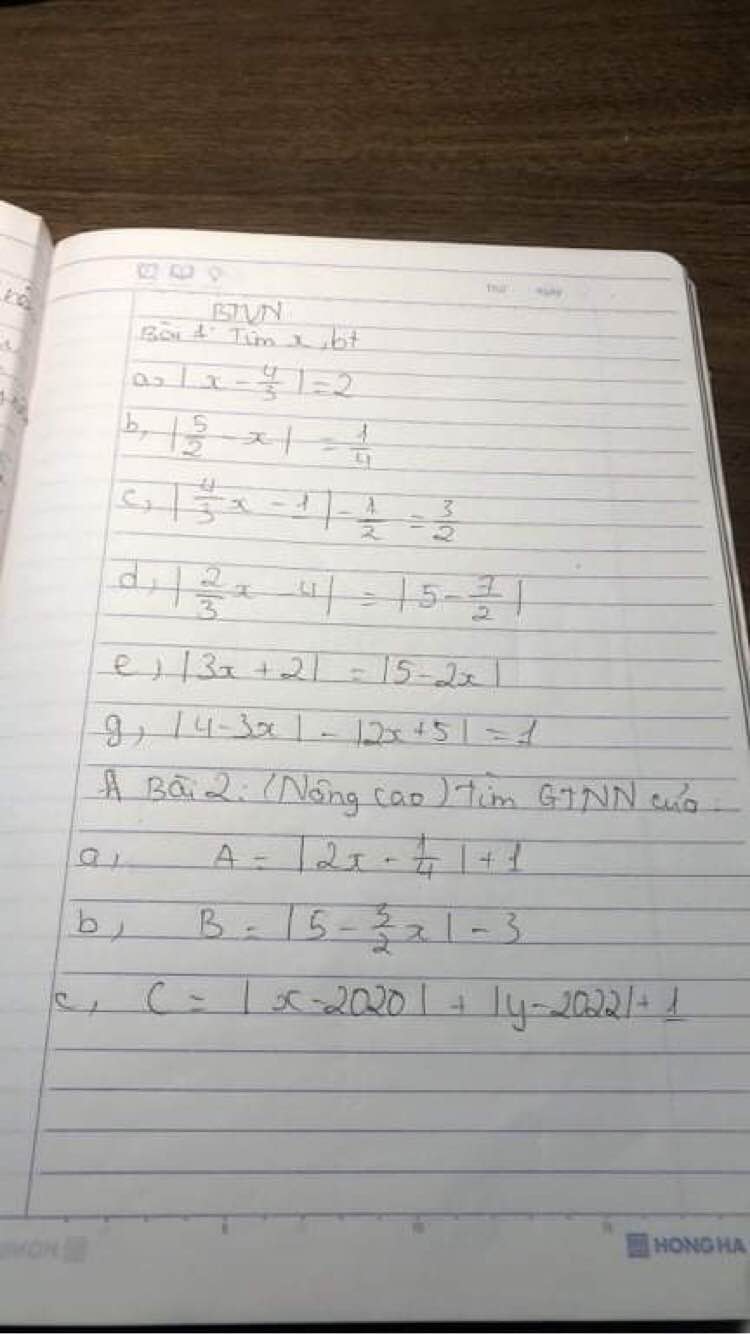
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2.
Do pt có 1 nghiệm bằng 2, thay \(x=2\) vào pt ta được:
\(2^2-2\left(m-1\right)-m=0\)
\(\Rightarrow6-3m=0\Rightarrow m=2\)
Khi đó nghiệm còn lại (tính theo định lý Viet là):
\(x_1x_2=-m\Rightarrow x_2=\dfrac{-m}{x_1}=\dfrac{-2}{2}=-1\)
x^2-(m-1)x-m=0 (*)
Ta có x=2 thế vào pt(*),ta có:
2^2-(m-1).2-m=0
<=> 4-2m+2-m=0
<=> -3m=-6
<=> m=2
Thế m=2 vào lại pt(*),ta lại có:
x^2-(2-1)x-2=0
<=> x^2-x-2=0
<=> x^2-2x+x-2=0
<=> (x^2-2x)+(x-2)=0
<=>x(x-2)+(x-2)=0
<=> (x-2)(x+1)=0
<=> x-2=0 hoặc x+1=0
<=>x=2 hoặc x=-1
Vậy S={−1;2}

Bài 4:
a: \(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
=-8

Câu c mình làm rồi: Mn ơi, hướng dẫn em cách để giống mẫu đi ạ! - Hoc24
\(d,\dfrac{x}{x^3-27}=\dfrac{x}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x\left(x-3\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x+2}{x^2-6x+9}=\dfrac{x+2}{\left(x-3\right)^2}=\dfrac{\left(x+2\right)\left(x^2+3x+9\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x-1}{x^2+3x+9}=\dfrac{\left(x-1\right)\left(x-3\right)^2}{\left(x-3\right)^2\left(x^2+3x+9\right)}\)
\(f,\dfrac{x+2}{x^2-3x+2}=\dfrac{x+2}{\left(x-1\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\\ \dfrac{x}{-2x^2+5x-3}=\dfrac{-x}{\left(2x-3\right)\left(x-1\right)}=\dfrac{-x\left(x-2\right)}{\left(2x-3\right)\left(x-1\right)\left(x-2\right)}\\ \dfrac{2x+1}{-2x^2+7x-6}=\dfrac{-\left(2x+1\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{-\left(2x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\)
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)}{\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(x+2a\right)\left(3x-2a\right)}\)
Do đó ta quy đồng:
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)

what is her mother going to prepare for her bỉthdat party

Bài 3:
2) Ta có: \(B=2x\left(y-z\right)+\left(z-y\right)\left(x+t\right)\)
\(=2x\left(y-z\right)-\left(x+t\right)\left(y-z\right)\)
\(=\left(y-z\right)\left(x-t\right)\)
\(=\left(24-10,6\right)\left(18,3+31,7\right)\)
\(=13,4\cdot50=670\)
3) Ta có: \(C=\left(x-y\right)\left(y+z\right)+y\left(y-x\right)\)
\(=\left(x-y\right)\left(y+z\right)-y\left(x-y\right)\)
\(=z\left(x-y\right)\)
\(=1.5\left(0.86-0.26\right)\)
\(=0,9\)

Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
i: \(x^2-9x+8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

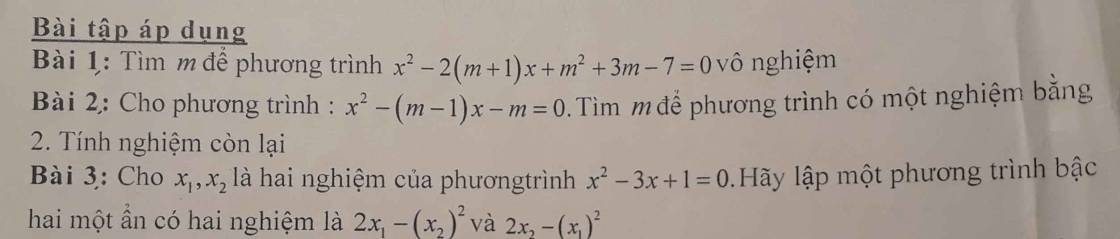



 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(


Bài 2:
a, A= | 2x - \(\dfrac{1}{4}\) | + 1
Ta có | 2x - \(\dfrac{1}{4}\) | ≥ 0 (∀x ∈ R)
⇒| 2x - \(\dfrac{1}{4}\) | + 1 ≥ 1
⇒ GTNN của A là 1
b, B= | 5 - \(\dfrac{3}{2}\)x | - 3
Ta có | 5 - \(\dfrac{3}{2}\)x | ≥ 0 (∀x ∈ R)
⇒ | 5 - \(\dfrac{3}{2}\)x | - 3 ≥ -3
⇒ GTNN của B là -3
c, C= |x - 2020| + |y - 2022| + 1
Ta có |x - 2020| ≥ 0 (∀x ∈ R)
|y - 2022| ≥ 0 (∀y ∈ R)
⇒|x - 2020| + |y - 2022| ≥ 0 (∀x,y ∈ R)
⇒|x - 2020| + |y - 2022| + 1 ≥ 1
⇒ GTNN của C là 1
a) ∣ 2x-1/4 ∣≥0 ∀ x =>∣ 2x-1/4∣+1≥1
'=' xay ra <=> 2x-1/4=0 <=> x=1/8
b) tương tự a đc GTNN = -3 khi x=10/3
c)∣ x-2020 ∣ ≥0 ∀ x
∣ y-2022 ∣ ≥0 ∀ y
=>∣ x-2020 ∣+∣ y-2022 ∣ +1 ≥1 ∀ x,y
'=' xay ra <=> x-2020=0 <=>x=2020
y-2022=0 <=>y=2022