cho đồ thị hàm số y=f(x) xác định vs mọi x và thoả mãn f(a+b)=f(ab) và f(-3)= -3. Tính f(2006)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2015
f(-3) = f(-3.1) = f(-3+ 1) = f(-2) => f(-3) = f(-2) = - 3
f(-2) = (-2.1) = f(-2+ 1) = f(-1) => f(-2) = f(-1) = -3
Tiếp tục như vậy, nhận xét f(- n) = f(-n.1 ) = f(-n +1) = ...= f(-1) = -3 Với n là số nguyên dương
Ta có f(2006) = f(-2006).(-1)] = f(-2006 + (-1)) = f(-2007) = -3
LH
0
NT
0
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
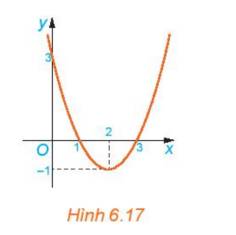
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
đúng và khẳng định 
sai.
sai và khẳng định 
đúng.
sai và khẳng định 
sai.
đúng và khẳng định 
đúng.
KV
14 tháng 1 2022
Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.
f(-3) = f(-3.1) = f(-3+ 1) = f(-2) => f(-3) = f(-2) = - 3
f(-2) = (-2.1) = f(-2+ 1) = f(-1) => f(-2) = f(-1) = -3
Tiếp tục như vậy, nhận xét f(- n) = f(-n.1 ) = f(-n +1) = ...= f(-1) = -3 Với n là số nguyên dương
Ta có f(2006) = f(-2006).(-1)] = f(-2006 + (-1)) = f(-2007) = -3
bài làm
f(-3) = f(-3.1) = f(-3+ 1) = f(-2) => f(-3) = f(-2) = - 3
f(-2) = (-2.1) = f(-2+ 1) = f(-1) => f(-2) = f(-1) = -3
f(- n) = f(-n.1 ) = f(-n +1) = ...= f(-1) = -3
Với n là số nguyên dương
Ta có f(2006) = f(-2006).(-1)] = f(-2006 + (-1)) = f(-2007) = -3
hok tốt