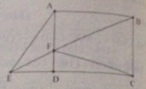
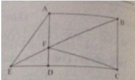
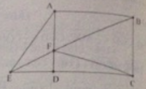
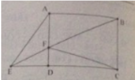
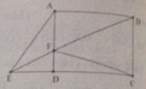
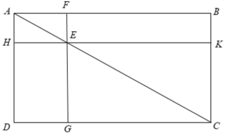
Cho hình chữ nhật ABCD (AB > AD), nối C với một điểm E bất kỳ trên đường chéo BD (\(BE<\frac{1}{2}BD\)), trên tia đối của EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với AB và AD (\(H\in AB,K\in AD\)). Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật
b) AF // BD ; KH // AC
c) Ba điểm E, H, K thẳng hàng

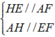 ⇒ AFEH là hình bình hành.
⇒ AFEH là hình bình hành.