cho tam giác ABC = tam giác DEH. Biết AB = 5cm, AC = 6cm, chu vi tam giác DEH bằng 19cm. Tính độ dài các cạnh của tam giác DEH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 2 2019
+) Do ΔABC = ΔDEH nên:
AB = DE = 5 cm
AC = DH= 6 cm
+) Vì chu vi tam giác DEH là 19 cm nên:
DE + EH + DH = 19
Thay số: 5 + EH +6 = 19 suy ra: EH = 8 cm
Vậy độ dài các cạnh của tam giác DEH là: DE = 5cm; DH = 6cm; EH = 8cm.
PA
30 tháng 10 2016
Tam giác ABC = Tam giác DEH (gt)
=> AB = DE (2 cạnh tương ứng) mà AB = 5 (cm) => DE = 5 (cm)
AC = DH (2 cạnh tương ứng) mà AC = 6 (cm) => DH = 6 (cm)
SDEH = 19
DE + DH + EH = 19
5 + 9 + EH = 19
EH = 19 - 9 - 5
EH = 5 (cm)
17 tháng 5 2021
Ta có tam giác ABC = tam giác MNP
=> AB = MN = 5 cm
=> AC = MP = 8 cm
Lại có : \(P_{MNP}=MN+NP+MP=20\)
\(\Rightarrow5+8+NP=20\Leftrightarrow NP=7\)cm
Vậy AB = 5 cm ; NP = 7 cm ; MP = 8 cm
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
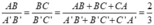
DE=5cm:DH=6cm:EH=8cm