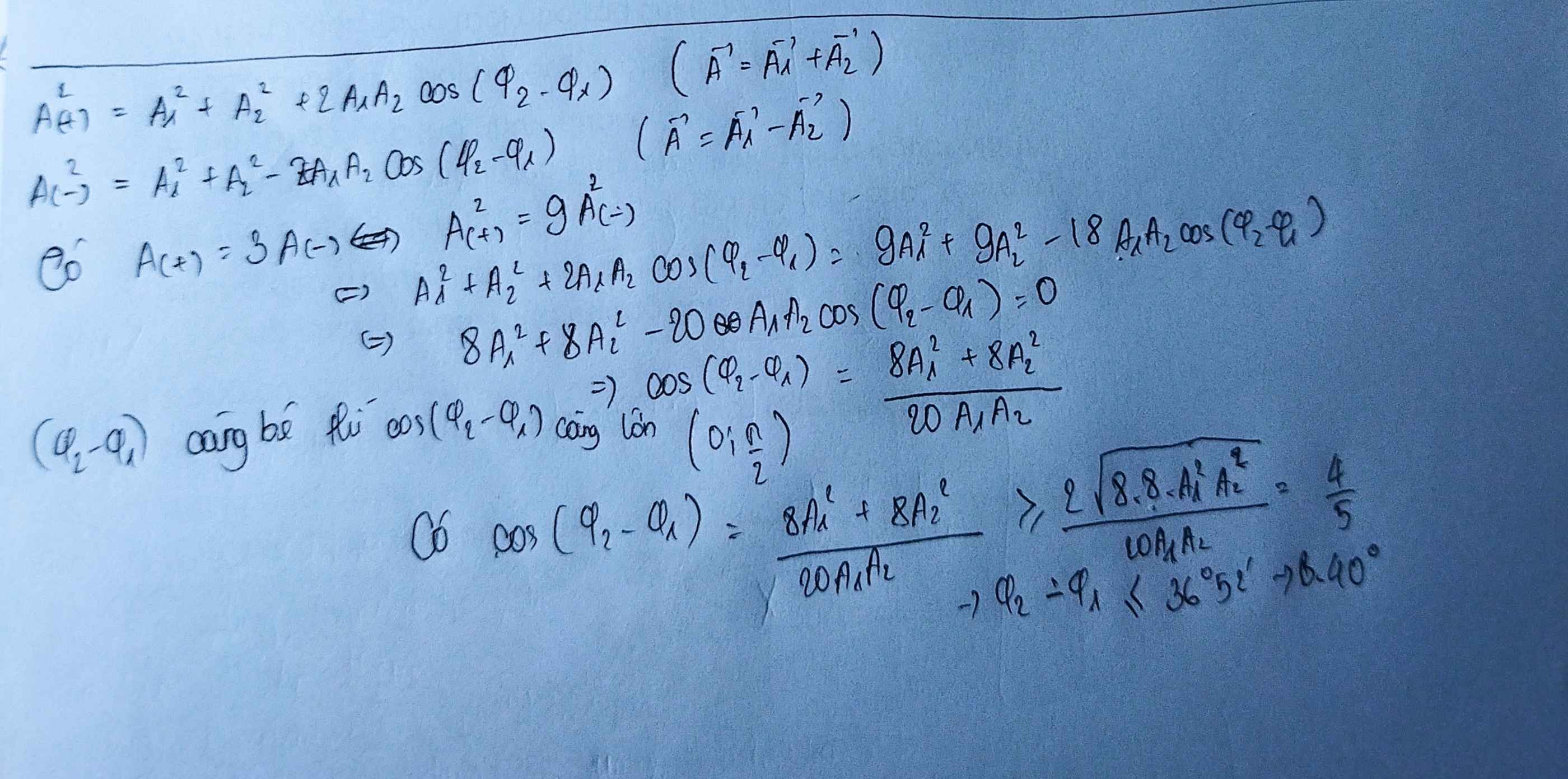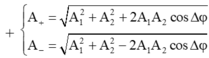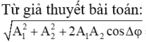Hai vật dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là x1=A1cos(ωt + φ1) và x2 = A2cos(ωt + φ2). Gọi x(+) = x1 + x2 và x(-) = x1 - x2. Biết rằng biên độ dao động của x(+) gấp 3 lần biên độ dao động của x(-). Độ lệch pha cực đại giữa x1 và x2 gần nhất với giá trị nào sau đây ?
A. 50° B. 40° C. 30° D. 60°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có:
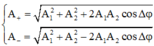
Từ giả thuyết bài toán:
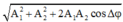
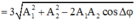
Biến đổi toán học ta thu được
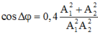
mặt khác
![]()
![]()
![]()

Biên độ dao động của x + và x - lần lượt là:
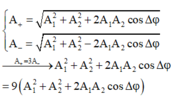
Biến đổi toán học để thu được biểu thức của cos ∆ φ
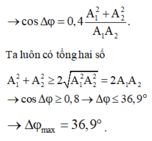
Đáp án B

Đáp án B
+ Biên độ dao động của x + và x - lần lượt là:
A + = A 1 2 + A 2 2 + 2 A 1 A 2 cos Δ φ A - = A 1 2 + A 2 2 - 2 A 1 A 2 cos Δ φ A 1 2 + A 2 2 + 2 A 1 A 2 cos Δ φ = 9 A 1 2 + A 2 2 + 2 A 1 A 2 cos Δ φ
+ Biến đổi toán học để thu được biểu thức của cos Δ φ → cos Δ φ = 0 , 4 A 1 2 + A 2 2 A 1 A 2 .
Ta luôn có tổng hai số
A 1 2 + A 2 2 ≥ 2 A 1 2 A 2 2 = 2 A 1 A 2 → cos Δ φ ≥ 0 , 8 → Δ φ ≤ 36 , 9 °
→ Δ φ max = 36 , 9 °

Đáp án A
Phương pháp: Sử dụng công thức tính biên độ dao động tổng hợp của hai dao động điều hoà cùng phương, cùng tần số

Đáp án D
+ Hai động động thành phần có độ lệch pha ∆ φ = ( 2 k + 1 ) π → hai dao động ngược pha => biên độ dao động tổng hợp đạt cực tiểu.