Tìm GTNN của A = x 2 +8x+10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=2x^2+8x-24\)
\(=2\left(x^2+4x-12\right)\)
\(=2\left[x^2+4x-4-8\right]\)
\(=2\left[\left(x-2\right)^2-8\right]\)
\(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2-8\ge-8\)
\(\Rightarrow2\left[\left(x-2\right)^2-8\right]\ge-16\)
Do đó GTNN của A là -16 khi \(x-2=0\Rightarrow x=2\)
\(B=x^2-8x+5=x^2-8x+16-9\)
\(=x^2-2\left(4x\right)+4^2-9\)
\(=\left(x-4\right)^2-9\)
\(\left(x-4\right)^2\ge0\)
\(\Rightarrow\left(x-4\right)^2-9\ge-9\)
Do đó GTNN của B là -9 khi \(x-4=0\Rightarrow x=4\)

1) \(A=x^2+8x+15=\left(x^2+8x+16\right)-1=\left(x+4\right)^2-1\ge-1\)
\(minA=-1\Leftrightarrow x=-4\)
2) \(B=7x-x^2-5=-\left(x^2-7x+\dfrac{49}{4}\right)+\dfrac{29}{4}=-\left(x-\dfrac{7}{2}\right)^2+\dfrac{29}{4}\le\dfrac{29}{4}\)
\(maxB=\dfrac{29}{4}\Leftrightarrow x=\dfrac{7}{2}\)


I zì:vv
a) Ta có: \(A=4x^2+4x+11=4x^2+4x+1=10=\left(2x+1\right)^2+10\ge10\forall x\)
Vậy MinA=10 khi \(x=-\dfrac{1}{2}\)
b) Ta có: \(B=5-8x-x^2=-\left(x^2+8x-5\right)=-\left(x^2+8x+16-21\right)\)
\(=-\left(x+4\right)^2+21\le21\forall x\)
Vậy MaxB=21 khi x=-4

a, \(A=2x^2-8x-10=2\left(x^2-4x+4\right)-18=2\left(x-2\right)^2-18\ge-18\)
Dấu "=" xảy ra <=> x-2=0 <=> x=2
Vậy MinA = -18 khi x=2
b, \(B=x-x^2=-\left(x^2-x+\frac{1}{4}\right)+\frac{1}{4}=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
Dấu "=" xảy ra <=> x-1/2=0 <=> x=1/2
Vậy MaxB = 1/4 khi x=1/2
a) \(A=2x^2-8x-10\)
\(=2\left(x^2-4x-5\right)\)
\(=2\left(x^2-2.x.2+2^2-2^2-5\right)\)
\(=2\left[\left(x-2\right)^2-9\right]\)
\(=2\left(x-2\right)^2-18\)
Vì \(2\left(x-2\right)^2\ge0\forall x\)
Nên \(2\left(x-2\right)^2\ge-18\)
Hay \(A\ge-18\)
Vậy gtnn của A là -18 khi \(2\left(x-2\right)^2=0\)
\(x-2=0\)
\(x=2\)
b) \(B=x-x^2\)
\(=-x^2-x\)
\(=-\left(x^2-x\right)\)
\(=-\text{[}x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\text{]}\)
\(=-\text{[}\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\text{]}\)
\(=-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\)
Vì \(-\left(x-\frac{1}{2}\right)^2\le0\forall x\)
Nên \(-\left(x-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\forall x
\)
Vậy gtln của B là \(\frac{1}{4}\)khi \(x-\frac{1}{2}=0\)
\(x=\frac{1}{2}\)


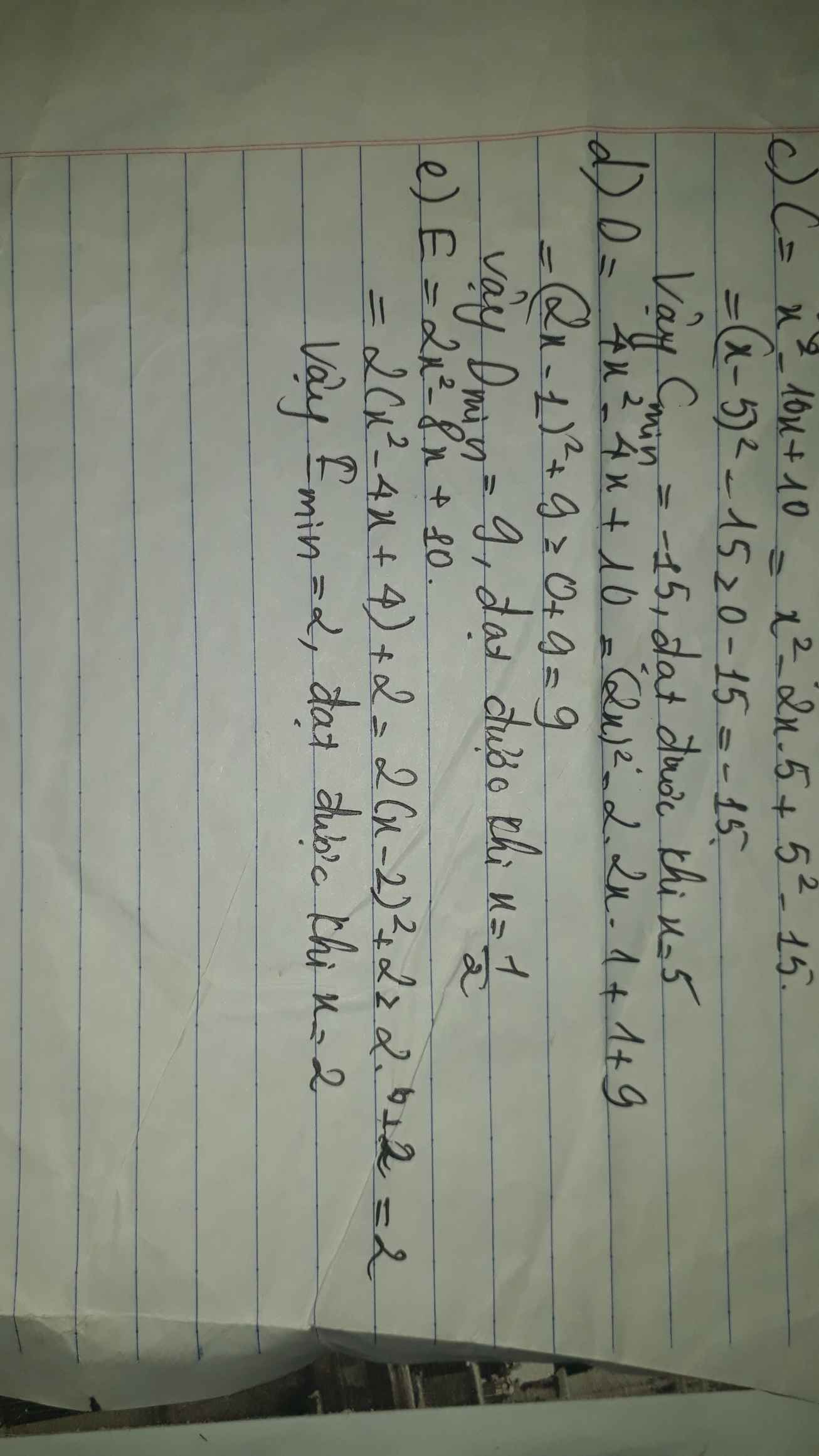
`A=x^2+8x+10`
`=x^2+2.x.4+4^2-6`
`=(x+4)^2-6`
Có: `(x+4)^2 >=0 forall x => (x+4)^2-6 >=-6`
`=> A_(min)=-6 <=> x=-4`.
\(x^2+8x+10=\left(x^2+8x+16\right)-16+10=\left(x+4\right)^2-6\)
Vì \(\left(x+4\right)^2\ge0\) nên \(A\ge-6\)
Vậy GTNN của A là -6
Dấu "=" xảy ra \(\text{⇔}x+4=0\text{⇔}x=-4\)