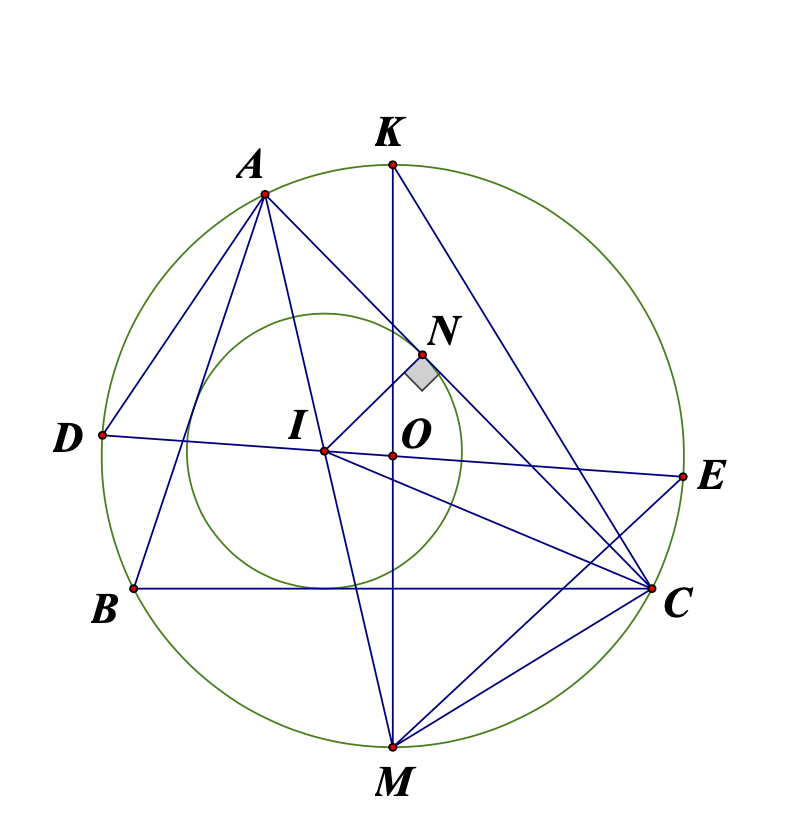
Cho tam giác ABC (AB < AC) nhọn nội tiếp đường tròn (O; R). Vẽ đường tròn (I; r) nội tiếp tam giác ABC. Vẽ dây AM của (O) qua I. Đường thẳng OI cắt (O) lần lượt tại D và E (I nằm giữa O và D).
a) Chứng minh: IA. IM = ID. IE và MI = MC
b) Chứng minh: MC = 2RsinMAC
please help... cảm ơn các bạnbạn

a) Vì ADME nội tiếp \(\Rightarrow\angle ADI=\angle IME\)
Xét \(\Delta IAD\) và \(\Delta IEM:\) Ta có: \(\left\{{}\begin{matrix}\angle AID=\angle EIM\\\angle ADI=\angle IME\end{matrix}\right.\)
\(\Rightarrow\Delta IAD\sim\Delta IEM\left(g-g\right)\Rightarrow\dfrac{IA}{IE}=\dfrac{ID}{IM}\Rightarrow IA.IM=ID.IE\)
ABMC nội tiếp \(\Rightarrow\angle MCB=\angle MAB=\dfrac{1}{2}\angle BAC\)
Ta có: \(\angle MCI=\angle MCB+\angle ICB=\dfrac{1}{2}\angle BAC+\dfrac{1}{2}\angle ACB\)
\(=\angle IAC+\angle ICA=\angle MIC\)
\(\Rightarrow\Delta MIC\) cân tại M \(\Rightarrow MI=MC\)
b) Kẻ \(OF\bot MC\Rightarrow F\) là trung điểm MC (\(\Delta OMC\) cân tại O)
\(\Rightarrow OF\) là phân giác \(\angle MOC\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOC=\dfrac{1}{2}.2\angle MAC=\angle MAC\)
\(\Rightarrow sinMOF=sinMAC\)
Ta có: \(MC=2MF=2.\dfrac{MF}{MO}.MO=2.sinMOF.R=2RsinMAC\)