Tứ giác ABCD có E, F , G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
Tứ giác EFGH là hình gì? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 8 2019
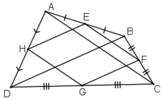
+ E là trung điểm AB, F là trung điểm BC
⇒ EF là đường trung bình của tam giác ABC
⇒ EF // AC và EF = AC/2
+ H là trung điểm AD, G là trung điểm CD
⇒ HG là đường trung bình của tam giác ACD
⇒ HG // AC và HG = AC/2.
+ Ta có:
EF //AC, HG//AC ⇒ EF // HG.
EF = AC/2; HG = AC/2 ⇒ EF = HG
⇒ tứ giác EFGH là hình bình hành.
CM
11 tháng 5 2017
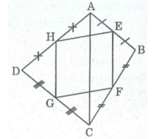
Nối đường chéo AC.
Trong ∆ ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ∆ ABC
⇒EF//AC và EF = 1/2 AC
(tính chất đường trung hình tam giác) (1)
Trong ∆ ADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
DT
2 tháng 8 2017
- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2)
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một)
=>Hình đó là hình bình hành
24 tháng 10 2017
À mà bạn tự vẽ hình nhé
Kẻ đường chéo AC(BD cũng được)
Xét tam giác ABC có: AE=EB:BF=CF
Do đó EF là đường trung bình của tam giác ABC
=>EF//AC:EF=1/2AC (1)
TTự: Xét tam giác ADC có: CG=DG:AH=DH
Do đó GH là đường trung bình của tam giác ADC
=>GH//AC:GH=1/2AC (2)
Từ (1) và (2) suy ra EF//GH:EF=GH
Vậy tứ giác EFGH là hình bình hành
Thấy đúng thì chia sẻ nha :D
26 tháng 9 2017
Xét \(\Delta ABC\) có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đường trung bình \(\Delta ABC\) (ĐN đường TB \(\Delta\))
=> EF // AC, \(EF=\dfrac{AC}{2}\) (tính chất đường TB \(\Delta\))
Xét \(\Delta ADC\) có:
H là trung điểm AD
G là trung điểm DC
=> HG là đường trung bình \(\Delta ADC\) (ĐN đường TB \(\Delta\))
=> HG // AC, \(HG=\dfrac{BC}{2}\) (tính chất đường TB \(\Delta\))
Ta có: EF // AC, HG // AC
\(EF=\dfrac{AC}{2},HG=\dfrac{AC}{2}\)
=> EF // HG, EF = HG
Xét tứ giác EFGH có:
EF // HG
EF = HG
=> EFGH là hình bình hành (dhnb)
HY
21 tháng 4 2017
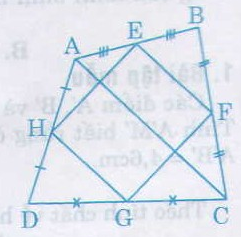
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
Suy ra EF // HG (1)
Tương tự EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = 1212AC.
HG là đường trung bình của ∆ACD nên HG = 1212AC.
Suy ra EF = HG
Lại có EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3).
CM
25 tháng 2 2019
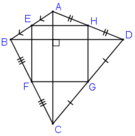
Ta có EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒EF // AC và EF = AC/2 (1)
HD = HA, GD = GC
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2 (2)
Từ (1) và (2) suy ra EF // HG và EF = HG
⇒ Tứ giác EFGH là hình bình hành (*)
EA = EB, HA = HD ⇒ EH là đường trung bình của ΔABD ⇒ EH // BD.
Mà EF // AC, AC ⊥ BD
⇒ EH ⊥ EF ⇒ Ê = 90º (**)
Từ (*) và (**) suy ra EFGH là hình chữ nhật.
C
4 tháng 1 2021
Xét ΔABC có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đường trung bình ΔABC (ĐN đường TB Δ)
=> EF // AC, EF=\(\dfrac{AC}{2}\) (tính chất đường TB Δ)
Xét ΔADC có:
H là trung điểm AD
G là trung điểm DC
=> HG là đường trung bình ΔADC (ĐN đường TB Δ)
=> HG // AC, HG=\(\dfrac{BC}{2}\) (tính chất đường TB Δ)
Ta có: EF // AC, HG // AC
EF=\(\dfrac{AC}{2}\),HG=\(\dfrac{AC}{2}\)
=> EF // HG, EF = HG
Xét tứ giác EFGH có:
EF // HG
EF = HG
=> EFGH là hình bình hành (dhnb)
A
4 tháng 1 2021
Xét tam giác ABC có: EB=EA (gt); BF=FC (gt)
EF là đường trung bình của tam giác ABC
EF//AC; EF=1/2AC (1)
Xét tam giác ADC có: AH=HD (gt); CG=DG (gt)
HG là dường trung bình của tam giác ADC
HG//AC; HG=1/2AC (2)
Từ (1) và (2) EF//HG; EF=HG
EFGH là hình bình hành
Ta có EH là đường trung bình của tam giác ABD
vì AE=EB; AH=HD
EH//BD
mà AC BD; EH=BD; EF//AC
EFEH hay E=
Vậy EFGH là hình chữ nhật.
Trả lời :
+ E là trung điểm AB, F là trung điểm BC
⇒ EF là đường trung bình của tam giác ABC
⇒ EF // AC và EF = \(\frac{AC}{2}\)
+ H là trung điểm AD, G là trung điểm CD
⇒ HG là đường trung bình của tam giác ACD
⇒ HG // AC và HG = \(\frac{AC}{2}\).
+ Ta có:
EF // AC, HG//AC ⇒ EF // HG.
EF = \(\frac{AC}{2}\); HG = \(\frac{AC}{2}\) ⇒ EF = HG
⇒ Tứ giác EFGH là hình bình hành.
ai biet