Bài 1:a) Giải bài toán bằng cách lập phương trình:Một hình chữ nhật có chiều dài hơn chiều rộng 7m, biết đường chéo hình chữ nhật là 13m. Tính chiều dài, chiều rộng của hình chữ nhậtb)Cho hệ phương trình \(\left\{{}\begin{matrix}x+my=3m\\mx-y=m^2-2\end{matrix}\right.\)tìm m để hệ phương trình có nghiệm duy nhất ( x;y) thỏa...
Đọc tiếp
Bài 1:
a) Giải bài toán bằng cách lập phương trình:
Một hình chữ nhật có chiều dài hơn chiều rộng 7m, biết đường chéo hình chữ nhật là 13m. Tính chiều dài, chiều rộng của hình chữ nhật
b)
Cho hệ phương trình \(\left\{{}\begin{matrix}x+my=3m\\mx-y=m^2-2\end{matrix}\right.\)
tìm m để hệ phương trình có nghiệm duy nhất ( x;y) thỏa mãn \(x^2-2x-y>-3\)
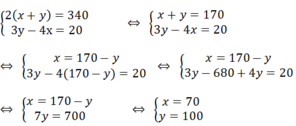
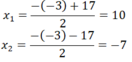
Bài 1 :
a, - Gọi chiều dài chiều rộng hình chữ nhật là x và y ( m, x>y> 0 )
Ta có : x - y = 7 ( I )
- Áp dụng định lý pitago ta có : \(x^2+y^2=13^2=169\left(II\right)\)
- Từ (I) và (II ) ta có hệ phương trình : \(\left\{{}\begin{matrix}x=y+7\\x^2+y^2=169\end{matrix}\right.\)
\(\Leftrightarrow y^2+y^2+14y+49=169\)
\(\Leftrightarrow2y^2+14y-120=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=5\left(TM\right)\\y=-12\left(L\right)\end{matrix}\right.\)
=>x = 5 + 7 = 12 (m )
Vậy ...