Cho x+y=a+b và x2+y2=a2+b2. Chứng minh: x3+y3=a3+b3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có x + y = a + b
=> (x + y)2 = (a + b)2
=> x2 + y2 + 2xy = a2 + b2 + 2ab
=> xy = ab
Lại có x + y = a + b
=> (x + y)3 = (a + b)3
=> x3 + 3x2y + 3xy2 + y3 = a3 + 3a2b + 3ab2 + b3
=> x3 + y3 + 3xy(x + y) = a3 + b3 + 3ab(a + b)
=> x3 + y3 = a3 + b3 (vì x + y = a + b ; xy = ab)

\(x+y=a+b\Leftrightarrow x^2+2xy+y^2=a^2+2ab+b^2\left(1\right)\)
\(x^3+y^3=a^3+b^3\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)=\left(a+b\right)^3-3ab\left(a+b\right)\)
mà do a+b=x+y nên \(ab=xy\) thay vào (1) ta có
\(x^2+y^2=a^2+b^2\)

Ta có:
\(a^3+2c=3ab\)
\(\Rightarrow\left(x+y\right)^3+2\left(x^3+y^3\right)=3\cdot\left(x+y\right)\left(x^2+y^2\right)\)
\(\Rightarrow\left(x^3+3x^2y+3xy^2+y^3\right)+2x^3+2y^3=3\left(x^3+xy^2+x^2y+y^3\right)\)
\(\Rightarrow x^3+3x^2y+3xy^2+y^3+2x^3+2y^3=3x^3+3xy^2+3xy^2+3y^3\)
\(\Rightarrow3x^3+3x^2y+3xy^2+3y^3=3x^3+3x^2y+3xy^2+3y^3\)
\(\Rightarrow\left(3x^3-3x^3\right)+\left(3x^2y-3x^2y\right)+\left(3xy^2-3xy^2\right)+\left(3y^3-3y^3\right)=0\)
\(\Rightarrow0=0\left(dpcm\right)\)
\(\Rightarrow0=0\left(\text{luôn đúng}\right)\)
Vậy, \(a^3+2c=3ab\)

VP `=(a+b)(a^2-ab+b^2)`
`=a^3-a^2b+ab^2+a^2b-ab^2+b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)+b^3`
`=a^3+b^3`
.
VP `=(a-b)(a^2+ab+b^2)`
`=a^3+a^2b+ab^2-a^2b-ab^2-b^3`
`=a^3+(a^2b-a^2b)+(ab^2-ab^2)-b^3`
`=a^3-b^3`

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

a A 3 2 4 1 c b B 3 2 4 1
a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)

Thực hiện phép nhân đa thức với đa thức ở vế trái.
=> VT = VP (đpcm)
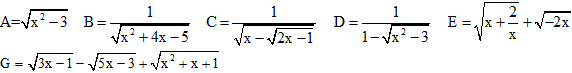 Mn giúp em với ;-;
Mn giúp em với ;-;
x+y=a+b => (x+y)2 = (a+b)2 <=> x2+y2+2xy=a2+b2+2ab mà x2+y2=a2+b2 nên ta suy ra xy=ab
ta có x3+y3 = (x+y)(x2-xy+y2) thay các dữ kiện đã có ta được x3+y3=(a+b)(a2-ab+b2)=a3+b3 điều phải chứng minh