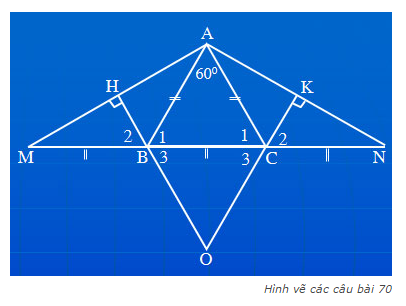
Cho \(\Delta ABC\). Trên tia đối tia BC lấy điểm M sao cho BM=BA, trên tia đối tia CB lấy điểm N sao cho CN=CA. Qua B, kẻ \(BH\perp AM\). Qua C, kẻ \(CK\perp AN\) (\(H\in AN\), \(K\in AN\)). Gọi O là giao điểm BH và CK. CMR:
a) O nằm trên đường trung trực của MN
b) AO là tia phân giác \(\widehat{BAC}\)

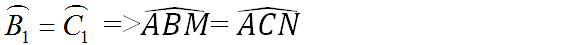

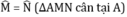
$BH, CK$ cùng vuông góc với $AN$ thì nó song song nhau. Như vậy thì $BH, CK$ làm sao giao nhau tại $O$ được?
Em xin lỗi, em chép sai đề bài. Còn đúng ra là \(BH\perp AM\), em có sửa lại đề bài rồi ạ!