câu a,b thôi ạ gaapspppppppppppppppppppppppppppppp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`a)P(x)+Q(x)=x^5-2x^2+1`
`=>Q(x)=x^5-2x^2+1-P(x)`
`=>Q(x)=x^5-2x^2+1-x^4+3x^2-1/2+x`
`=>Q(x)=x^5-x^4+x^2+x+1/2`
______________________________________________
`b)P(x)-R(x)=x^3`
`=>R(x)=P(x)-x^3`
`=>R(x)=x^4-3x^2+1/2-x-x^3`
`=>R(x)=x^4-x^3-3x^2-x+1/2`
Ta có:
\(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)
\(\Rightarrow Q\left(x\right)=P\left(x\right)-\left(x^5-2x^2+1\right)\)
\(=x^4-3x^2+\dfrac{1}{2}-x-x^5+2x^2-1\)
\(=-x^5+x^4-x^2-x-\dfrac{1}{2}\)
Vậy \(Q\left(x\right)=-5^2+x^4-x^2-x-\dfrac{1}{2}\)

b Ta có \(\Lambda ABE=\dfrac{1}{2}sđ\cap BE,\Lambda AFB=\dfrac{1}{2}sđ\cap BE\Rightarrow\Lambda ABE=\Lambda AFB\)
Mà \(\Lambda EAB=\Lambda BAF\) \(\Rightarrow\Delta EAB\sim\Delta BAF\left(g.g\right)\Rightarrow\dfrac{EA}{BA}=\dfrac{AB}{ÀF}\Rightarrow AE\cdot AF=AB^2\left(1\right)\)
Áp dụng hệ thức lượng giác vào \(\Delta AOB\) có:(BH vuông góc với AO)
\(\Rightarrow AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AH\cdot AO=AE\cdot AF\)
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là tứ giác nội tiếp
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{BFE}\) là góc nội tiếp chắn \(\stackrel\frown{BE}\)
\(\widehat{ABE}\) là góc tạo bởi dây cung BE và tiếp tuyến BA
Do đó: \(\widehat{BFE}=\widehat{ABE}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
\(\Leftrightarrow\widehat{BFA}=\widehat{EBA}\)
Xét ΔBFA và ΔEBA có
\(\widehat{BFA}=\widehat{EBA}\)(cmt)
\(\widehat{ABF}\) là góc chung
Do đó: ΔBFA∼ΔEBA(g-g)
\(\Leftrightarrow\dfrac{AF}{AB}=\dfrac{AB}{AE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AF\cdot AE\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBOA vuông tại B có BH là đường cao ứng với cạnh huyền AO, ta được:
\(AB^2=AH\cdot AO\)(2)
Từ (1) và (2) suy ra \(AF\cdot AE=AH\cdot AO\)(đpcm)

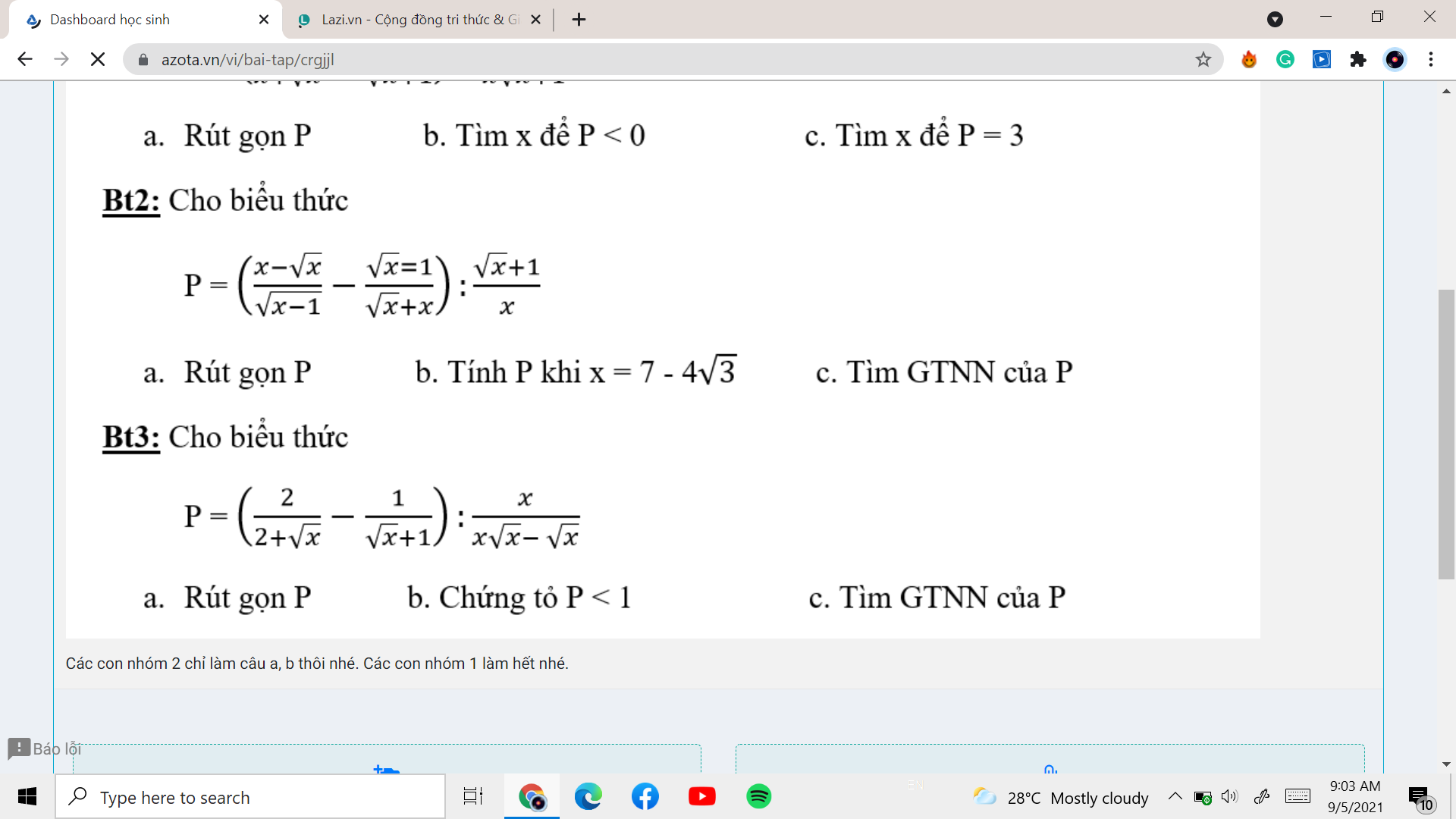
Bài 3:
a: Ta có: \(P=\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x}{x\sqrt{x}-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+2-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)

b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)


a) Có \(\widehat{OAM}=90^0\) => Tam giác \(OAM\) nội tiếp đường tròn đường kính OM
=> O,A,M cùng thuộc đường tròn đường kính OM (*)
Có \(\widehat{OBM}=90^0\) => Tam giác \(OBM\) nội tiếp đường tròn đường kính OM
=> O,B,M cùng thuộc đường tròn đường kính OM (2*)
Do N là trung điểm của PQ => \(ON\perp PQ\)( Vì trong một đt, đường kính đi qua trung điểm của một dây ko đi qua tâm thì vuông góc với dây ấy)
=> \(\widehat{ONM}=90^0\) => Tam giác \(ONM\) nội tiếp đường tròn đường kính OM
=> O,N,M cùng thuộc đt đường kính OM (3*)
Từ (*) (2*) (3*) => O,M,N,A,B cùng thuộc đt đk OM hay đt bán kính \(\dfrac{OM}{2}\)
b) Có AM//PS (cùng vuông góc với OA)
Gọi E là gđ của PS với (O) => \(sđ\stackrel\frown{AE}=sđ\stackrel\frown{AP}\)
Có \(\widehat{PRB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AE}+sđ\stackrel\frown{PB}\right)\)\(=\dfrac{1}{2}\left(sđ\stackrel\frown{AP}+sđ\stackrel\frown{PB}\right)=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
=> \(\widehat{PRB}=\widehat{MAB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
Có BNAM nội tiếp => \(\widehat{MAB}=\widehat{MNB}\)
\(\Rightarrow\widehat{PRB}=\widehat{MNP}\) => PRNB nội tiếp
\(\Rightarrow\widehat{BRN}=\widehat{BPN}\) mà \(\widehat{BPN}=\widehat{BAQ}=\dfrac{1}{2}sđ\stackrel\frown{BQ}\)
\(\Rightarrow\widehat{BRN}=\widehat{BAQ}\) => RN//AQ hay RN // SQ mà N la trung điểm của PQ
=> RN là đường TB của tam giác PSQ
=> R là trung điểm của PS <=> PR=RS

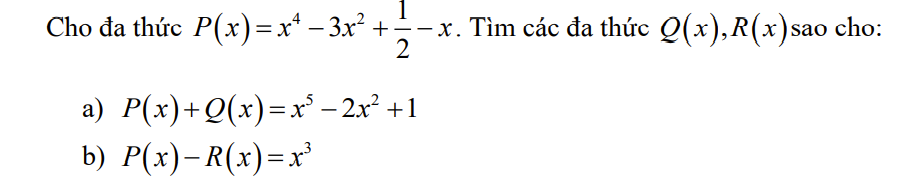





a,theo giả thiết E lần lượt là hình chiếu của H lên AB,
H là chân đường vuông góc kẻ từ B xuống AC
\(=>\)\(\angle\left(BEH\right)=\angle\left(BHA\right)=90^o\)
có \(\angle\left(B\right)chung\)\(=>\Delta BEH\sim\Delta BHA\left(g.g\right)\left(dpcm\right)\)
b, ta có E,F là hình chiếu của H trên AB,BC
\(=>HE\perp AB,HF\perp BC\)
mà \(BH\perp AC\left(gt\right)=>\)\(\Delta BHA\) vuông tại H có HE là đường cao
và \(\Delta BHC\) vuông tại H có HF là đường cao
theo hệ thức lượng
\(=>BH^2=BE.BA=BF.BC\left(dpcm\right)\)