Hãy chứng minh định lí Pom-piu : Ở miền trong 1 tam giác đều, cứ lấy 1 điểm bất kì thì khoảng cách từ điểm đó đến 3 đỉnh của tam giác thỏa mãn độ dài 3 cạnh của 1 tam giác ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2021
Xét tam giác ABC, M là điểm trong tam giác, MD,ME,MF lần lượt là hình chiếu của M lên AB,AC,BC
Kẻ đường cao AH const
Đặt \(AB=AC=BC=a\)
\(S_{ABC}=S_{AMB}+S_{AMC}+S_{BMC}\)
\(=\frac{1}{2}\left(DM.AB+ME.AC+MF.BC\right)\)
\(=\frac{1}{2}a\left(DM+ME+MF\right)\)
\(=\frac{1}{2}a.AH\)
\(=DM+ME+MF=AH\left(đpcm\right)\)
27 tháng 12 2021
Xét tam giác ABC, M là điểm trong tam giác, MD,ME,MF lần lượt là hình chiếu của M lên AB,AC,BC
Kẻ đường cao \(AH\) const
Đặt \(AB=AC=BC=a\)
\(S_{ABC}=S_{AMB}+S_{AMC}+S_{BMC}\\ =\dfrac{1}{2}\left(DM.AB+ME.AC+MF.BC\right)\\ =\dfrac{1}{2}a\left(DM+ME+MF\right)\\ =\dfrac{1}{2}a.AH\\ \Rightarrow DM+ME+MF=AH\\ \RightarrowĐpcm\)
AT
16 tháng 8 2015
|
|
14 tháng 7 2018
Cho M nằm trong tam giác đều ABC chứng minh 1 trong 3 đoạn thẳng MA ,MB ,MC nhỏ hơn tổng 2 đoạn thẳng còn lại
CM
24 tháng 5 2017
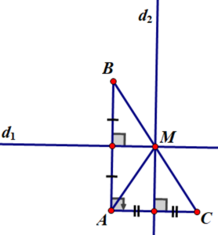
+ Giả sử ∆ABC vuông tại A.
d1 là đường trung trực cạnh AB, d2 là đường trung trực cạnh AC.
d1 cắt d2 tại M. Khi đó M là điểm cách đều ba đỉnh của tam giác ABC.
+ Áp dụng kết quả bài 55 ta có B, M, C thẳng hàng.
QUẢNG CÁO+ M cách đều A, B, C ⇒ MB = MC ⇒ M là trung điểm của cạnh BC (đpcm)
+ M là trung điểm của cạnh BC (đpcm)
*) Giả sử AM là trung tuyến của tam giác ABC suy ra M là trung điểm của cạnh BC
⇒ MB = MC = BC/2
Mà MA = MB = MC (cmt)
⇒ MA = BC/2
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.