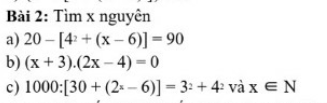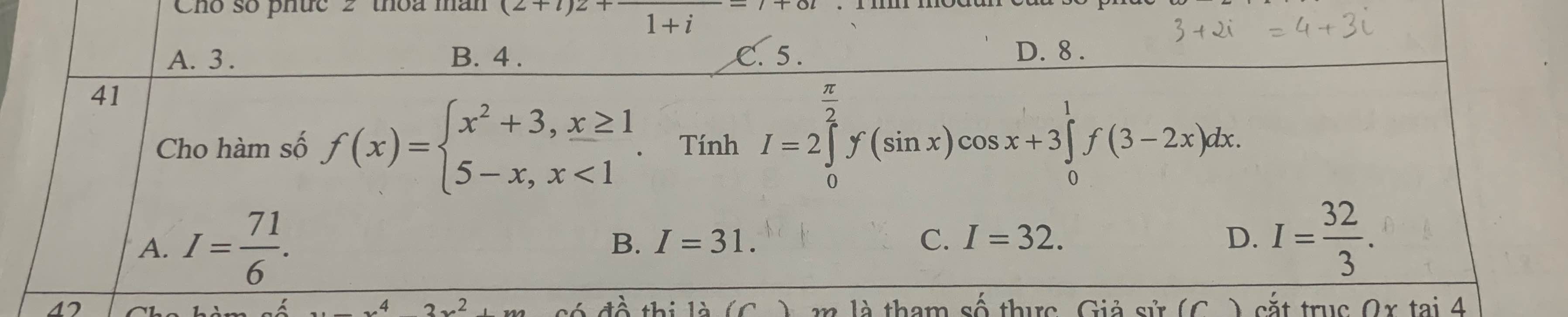Ai giúp mình với !! Mình cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ai giúp mình với ạ, mình cảm ơn rất nhiều
3 tháng 7 2021
Gọi điện trở ampe kế là Ra
Hiệu điện thế hai đầu ampe kế A2 là:
\(UA2=I2.Ra=1.Ra=Ra\)
Mà ta lại có: \(UA2=UA3+IA3.2r=IA3.Ra+IA3.2r=0.5Ra+0.5.2r=0.5Ra+r\)
=> \(Ra=0.5Ra+r\)
=> \(r=0.5Ra\)
Ta có: \(IMP=IA2+IA3=1+0.5=1.5\left(A\right)\)
=>\(UMP=IMP.r=1.5r=1,5.0.5Ra=0.75Ra\)
=>\(UMQ=UMP+UA2=0.75Ra+Ra=1.75Ra\)
=> Cường độ dong điện chạy qua ampe kế A1 là:
\(IA1=\dfrac{UMQ}{Ra}=\dfrac{1.75Ra}{Ra}=1.75\left(A\right)\)
S
3 tháng 3
CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
23 tháng 12 2021
c)\(\left\{{}\begin{matrix}u_1+u_3=3\\u_1^2+u_3^2=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\\left(u_1+u_3\right)^2-2u_1u_3=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\u_1u_3=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}u_1=2\\u_3=1\end{matrix}\right.\\\left\{{}\begin{matrix}u_1=1\\u_3=2\end{matrix}\right.\end{matrix}\right.\)
Làm nốt (sử dụng công thức: \(u_n=u_1+\left(n-1\right)d\) để tìm được công sai
\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d\) để tính tổng 15 số hạng đầu)
d)\(\left\{{}\begin{matrix}u_1+u_2+u_3=14\\u_1u_2u_3=64\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_2-d+u_2+u_2+d=14\\\left(u_2-d\right)u_2\left(u_2+d\right)=64\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_2=\dfrac{14}{3}\\\left(u_2^2-d^2\right)u_2=64\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\dfrac{14}{3}=u_2=u_1+d\\d=\dfrac{2\sqrt{889}}{21}\end{matrix}\right.\\\left\{{}\begin{matrix}\dfrac{14}{3}=u_1+d\\d=\dfrac{-2\sqrt{889}}{21}\end{matrix}\right.\end{matrix}\right.\)
(Làm nốt,số xấu quá)
e)\(\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1^2+u_2^2+u_3^2=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1u_2u_3=\dfrac{21-\left(u_1+u_2+u_3\right)^2}{2}=-14\end{matrix}\right.\)
Làm như ý d)
13 tháng 10 2021
Bài 9:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-3=-3x+7\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)