Điểm cực đại của hàm số y = \(\dfrac{x}{\sqrt{2x^2+9}-1}\) là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
Nguyễn Đức Trí
VIP
15 tháng 9 2023
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2021
1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2021
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
a. Hàm có 3 cực trị \(\Rightarrow m< 0\)
\(y'=8x^3+4mx=4x\left(2x^2+m\right)=0\Rightarrow\left[{}\begin{matrix}x=0;y=-\dfrac{3m}{2}\\x=-\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\\x=\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\end{matrix}\right.\)
Trong đó \(A\left(0;-\dfrac{3m}{2}\right)\) là cực đại và B, C là 2 cực tiêu
Do tam giác ABC luôn cân tại A \(\Rightarrow\) tâm I của đường tròn ngoại tiếp luôn nằm trên trung trực BC hay luôn nằm trên Oy
Mà tứ giác ABCO nội tiếp \(\Rightarrow OI=AI\Rightarrow I\) là trung điểm OA (do I, O, A thẳng hàng, cùng nằm trên Oy)
\(\Rightarrow I\left(0;-\dfrac{3m}{4}\right)\)
Mặt khác trung điểm BC cũng thuộc Oy và IB=IC (do I là tâm đường tròn ngoại tiếp)
\(\Rightarrow\) I trùng trung điểm BC
\(\Rightarrow-\dfrac{3m}{4}=-\dfrac{m^2+3m}{2}\) \(\Rightarrow m\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
b.
Từ câu a ta thấy khoảng cách giữa 2 cực đại là:
\(\left|x_B-x_C\right|=2\sqrt{-\dfrac{m}{2}}=5\Rightarrow m=-\dfrac{25}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Xét trên các miền xác định của các hàm (bạn tự tìm miền xác định)
a.
\(y'=\dfrac{1}{2\sqrt{x-3}}-\dfrac{1}{2\sqrt{6-x}}=\dfrac{\sqrt{6-x}-\sqrt{x-3}}{2\sqrt{\left(x-3\right)\left(6-x\right)}}\)
\(y'=0\Rightarrow6-x=x-3\Rightarrow x=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}\) là điểm cực đại của hàm số
b.
\(y'=1-\dfrac{9}{\left(x-2\right)^2}=0\Rightarrow\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực đại, \(x=5\) là điểm cực tiểu
c.
\(y'=\sqrt{3-x}-\dfrac{x}{2\sqrt{3-x}}=0\Rightarrow2\left(3-x\right)-x=0\)
\(\Rightarrow x=2\)
\(x=2\) là điểm cực đại
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
d.
\(y'=\dfrac{-x^2+4}{\left(x^2+4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(x=-2\) là điểm cực tiểu, \(x=2\) là điểm cực đại
e.
\(y'=\dfrac{-8\left(x^2-5x+4\right)}{\left(x^2-4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x=1\) là điểm cực tiểu, \(x=4\) là điểm cực đại
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)
2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)
3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)
ND
Nguyễn Đức Trí
VIP
17 tháng 9 2023
1) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
2) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1\left(x+9\right)}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-6}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(1\right)=\dfrac{-6}{\left(1+3\right)^2}+\dfrac{2}{\sqrt[]{1}}=-\dfrac{3}{8}+2=\dfrac{13}{8}\)
CM
7 tháng 11 2019
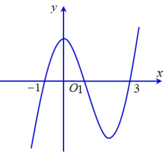
Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B
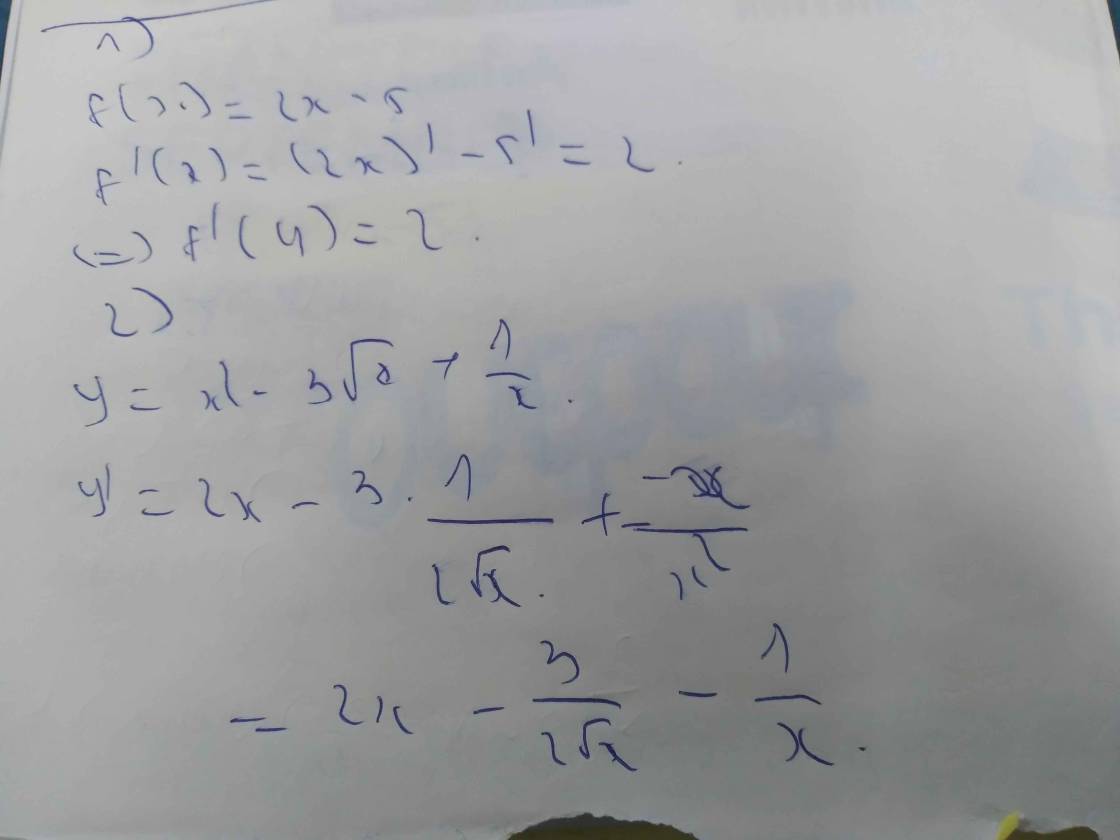
- Ảnh vỡ tke nhỉ ?