Cho 3m -2m =1.Biết m,n thuộc N. Chứng tỏ rằng m,n nguyên tố cùng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
IL
1
PT
1
CM
19 tháng 2 2019
Gọi ƯCLN (2m;2m+1)=d
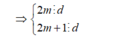
(2m+1) -2m ⋮ d → 1 ⋮ d → d=1
ƯCLN(2m,2m+1) =1
Vậy 2m và 2m+1 là số nguyên tố cùng nhau
TN
2
A
12 tháng 11 2015
GỌi d là ƯC(2m+1,2m)
=>2m chia hết cho d
=>2m+1 chia hết cho d
=> (2m+1)-(2m) chia hết cho d
=>1 chia hết cho d
=> d =1
vậy 2m và 2m+1 là 2 số nguyên tố cùng nhau
NN
2
15 tháng 12 2016
Giải:
Gọi \(d=UCLN\left(n+1;3n+4\right)\)
Ta có:
\(n+1⋮d\Rightarrow3n+3⋮d\)
\(3n+4⋮d\)
\(\Rightarrow3n+4-3n+3⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=UCLN\left(n+1;3n+4\right)=1\)
\(\Rightarrow n+1\) và 3n + 4 là 2 số nguyên tố cùng nhau
Vậy...
15 tháng 11 2017
CMR: n+1 & 3n+4 là 2 số nguyên tố cùng nhau
G/s: ƯCLN(n+1;3n+4) = d
Ta có:
n+1 =>3.(n+1) =>3n+3
3n+4=>1.(3n+4)=>3n+4
=> (3n+4) - (3n+3) \(⋮\) d
=> 3n+4 - 3n-3 \(⋮\) d
=> 1 \(⋮\) d => d \(\in\) ƯC(1) = \(\left\{1\right\}\)
KL: Vậy n+1 & 3n+4 là 2 số nguyên tố cùng nhau
14 tháng 11 2015
a chia hết cho m
a chia hết cho n
Nên a là BC(m;n)=m.n suy ra a chia hết cho m.n
LP
0
$3m-2m=1$ thì $m=1$. Còn $n$ ở đâu bạn?