CHO TAM GIÁC ABC CÂN TẠI A
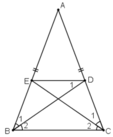
A/ĐƯỜNG PHÂN GIÁC BD,EC (D ∈ AC ,E ∈ AB).CMR TỨ GIÁC BEDC LÀ HÌNH THANG CÂN CÓ CẠNH BÊN BẰNG ĐÁY NHỎ
B/ĐƯỜNG CAO BH,CK (H ∈ AC, K ∈ AB).CMR: BKHC LÀ HÌNH THANG CÂN
C/ĐƯỜNG TRUNG TUYẾN BM ,CN (M ∈ AC, N ∈ AB). CMR :BNCM LÀ HÌNH THANG CÂN

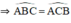
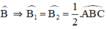
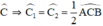
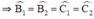
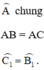
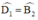 (Hai góc so le trong)
(Hai góc so le trong)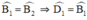 ⇒ ΔEDB cân tại E ⇒ ED = EB.
⇒ ΔEDB cân tại E ⇒ ED = EB.
a) Ta có \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\left(1\right)\)
Do BD là phân giác \(\widehat{ABC}\)\(\Rightarrow\widehat{ABD}=\widehat{DBC}\)
CE là phân giác \(\widehat{ACB}\)\(\Rightarrow\widehat{ACE}=\widehat{ECB}\)
Mà \(\Delta ABC\)cân \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Suy ra \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)( tự xét nha :)))
\(\Rightarrow AD=AE\)\(\Rightarrow\Delta AED\)cân tại A
\(\Rightarrow\widehat{AED}=\frac{180^o-\widehat{BAC}}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ABC}\)
Mà hai góc đó ở vị trí đồng vị
\(\Rightarrow ED//BC\)
Lại có : \(\widehat{ABC}=\widehat{ACB}\)
Suy ra : BEDC là hình thang cân (3)
Ta có : \(ED//BC\Rightarrow\widehat{EDB}=\widehat{DBC}\)( so le trong )
Mà \(\widehat{EBD}=\widehat{DBC}\)
Suy ra \(\widehat{EDB}=\widehat{EBD}\)\(\Rightarrow\Delta BED\)cân tại E
\(\Rightarrow EB=ED\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\)BEDC là hình thang cân có cạnh bên bằng đáy nhỏ -_-
b) Xét \(\Delta ABH=\Delta ACK\left(ch-gn\right)\)( tự xét )
\(\Rightarrow AK=AH\)\(\Rightarrow\Delta AKH\)cân tại A
\(\Rightarrow\widehat{AKH}=\frac{180^o-\widehat{BAC}}{2}\left(5\right)\)
Từ (1) và (5) \(\Rightarrow\widehat{AKH}=\widehat{ABC}\)
Mà hai góc trên ở vị trí đồng vị
Suy ra : KH // BC
Lại có : \(\widehat{ABC}=\widehat{ACB}\)
Suy ra : BKHC là hình thang cân
c) Do BM là trung tuyến \(\Rightarrow AM=\frac{1}{2}AC\)
CN là trung tuyến \(\Rightarrow AN=\frac{1}{2}AB\)
Mà AB = AC \(\Rightarrow AN=AM\)
\(\Rightarrow\Delta AMN\)cân tại A \(\Rightarrow\widehat{ANM}=\frac{180^o-\widehat{BAC}}{2}\left(6\right)\)
Từ (1) và (6) \(\Rightarrow\widehat{ANM}=\widehat{ABC}\)
Mà hai góc trên ở vị trí đồng vị
\(\Rightarrow MN//BC\)
Lại có : \(\widehat{ABC}=\widehat{ACB}\)
Suy ra BNMC là hình thang cân
Vậy ...