x2(2x+3)-8x-12=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YN
5 tháng 4 2022
`Answer:`
Bài 1:
a) \(7+2x=22-3x\)
\(\Leftrightarrow2x+3x=22-7\)
\(\Leftrightarrow5x=15\)
\(\Leftrightarrow x=3\)
b) \(8x-3=5x+12\)
\(\Leftrightarrow8x-5x=12+3\)
\(\Leftrightarrow3x=15\)
\(\Leftrightarrow x=5\)
c) \(x-12+4x=25+2x-1\)
\(\Leftrightarrow x-12+4x-25-2x+1=0\)
\(\Leftrightarrow\left(x+4x-2x\right)+\left(1-12-25\right)=0\)
\(\Leftrightarrow3x-36=0\)
\(\Leftrightarrow x=12\)
d) \(x+2x+3x-19=3x+5\)
\(\Leftrightarrow6x-19=3x+5\)
\(\Leftrightarrow6x-3x=5+19\)
\(\Leftrightarrow3x=24\)
\(\Leftrightarrow x=8\)
Bài 2:
a) \(\left(2,3x-6,9\right)\left(0,1x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2,3x-6,9=0\\0,1x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-20\end{cases}}}\)
b) \(\left(2x+7\right)\left(x-5\right)\left(5x+1\right)=0\)
\(\Leftrightarrow2x+7=0\text{ hoặc }x-5=0\text{ hoặc }5x+1=0\)
\(\Leftrightarrow x=-\frac{7}{2}\text{ hoặc }x=5\text{ hoặc }x=-\frac{1}{5}\)
c) \(\left(4x+2\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x+2=0\\x^2+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x^2=-1\text{(Loại)}\end{cases}}}\)
d) \(\left(x^2-4\right)+\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow x^2-4+\left(3x-2x^2-6+4x\right)=0\)
\(\Leftrightarrow x^2-4=\left(-2x^2+7x-6\right)=0\)
\(\Leftrightarrow x^2-4-2x^2+7x-6=0\)
\(\Leftrightarrow-x^2+7x-10=0\)
\(\Leftrightarrow x^2-5x-2x+10=0\)
\(\Leftrightarrow x.\left(x-5\right)-2.\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right).\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\\x=2\end{cases}}}\)
4 tháng 1 2022
a: \(=\dfrac{x^2+3x+2-x^2+2x+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)
b: \(=\dfrac{x^2-4x+3-x^2-3x-2+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)
c: \(=\dfrac{x+2}{x\left(x-2\right)}+\dfrac{2}{x\left(x+2\right)}+\dfrac{3x+2}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+2x+2x-4+3x+2}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+7x-2}{x\left(x-2\right)\left(x+2\right)}\)
DT
4 tháng 1 2022
a,
\(\dfrac{x+1}{x-2}-\dfrac{x}{x+2}+\dfrac{8}{x^2-4}\\ =\dfrac{x^2+3x+2-x^2+2x+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)
b,
\(\dfrac{x-3}{x+1}-\dfrac{x+2}{x-1}+\dfrac{8x}{x^2-1}\\ =\dfrac{x^2-4x+3-x^2-3x-2+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{1}{x-1}\)
29 tháng 10 2021
a: \(\Leftrightarrow\left(x-5\right)\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\\x=1\end{matrix}\right.\)
d: \(\Leftrightarrow\left(x+3\right)\left(x^2-4x+5\right)=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3
8 tháng 9 2023
a) \(4x^2-16+\left(3x+12\right)\left(4-2x\right)\)
\(=\left(2x-4\right)\left(2x+4\right)-3\left(x+4\right)\left(2x-4\right)\)
\(=\left(2x-4\right)\left(2x+4-3x-12\right)\)
\(=-\left(2x-4\right)\left(x+8\right)\)
b) \(x^3+x^2y-15x-15y\)
\(=x^2\left(x+y\right)-15\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-15\right)\)
c) \(3\left(x+8\right)-x^2-8x\)
\(=3\left(x+8\right)-x\left(x+8\right)\)
\(=\left(x+8\right)\left(3-x\right)\)
d) \(x^3-3x^2+1-3x\)
\(=x^3+1-3x^2-3x\)
\(=\left(x+1\right)\left(x^2-x+1\right)-3x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x+1-3x\right)\)
\(=\left(x+1\right)\left(x^2-4x+1\right)\)
d) \(5x^2-5y^2-20x+20y\)
\(=5\left(x^2-y^2\right)-20\left(x-y\right)\)
\(=5\left(x-y\right)\left(x+y\right)-20\left(x-y\right)\)
\(=5\left(x-y\right)\left(x+y-4\right)\)
DN
1
30 tháng 8 2023
\(a.x^2-7x-3x+21=0\Leftrightarrow\left(x^2-7x\right)-\left(3x-21\right)=0\)
\(\Leftrightarrow x\left(x-7\right)-3\left(x-7\right)=0\Leftrightarrow\left(x-3\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=7\end{matrix}\right.\)
\(b.x^2+6x+2x+12=0\Leftrightarrow\left(x^2+6x\right)+\left(2x+12\right)=0\)
\(\Leftrightarrow x\left(x+6\right)+2\left(x+6\right)=0\Leftrightarrow\left(x+2\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-6\end{matrix}\right.\)
\(c.x^2+4x+5x+20=0\Leftrightarrow\left(x^2+4x\right)+\left(5x+20\right)=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\Leftrightarrow\left(x+5\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\end{matrix}\right.\)
26 tháng 11 2022
a: ĐKXĐ của A là x<>1; x<>-3
ĐKXĐ của B là x<>4
ĐKXĐ của C là x<>0; x<>2
ĐKXĐ của D là x<>3
ĐKXĐ của E là x<>0; x<>2
b: \(A=\dfrac{2x\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}=\dfrac{2x}{x-1}\)
Để A=0 thì 2x=0
=>x=0
\(B=\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)^2}=\dfrac{x+4}{x-4}\)
Để B=0 thì x+4=0
=>x=-4
\(C=\dfrac{x\left(x+2\right)}{x\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Để C=0 thì x+2=0
=>x=-2
\(D=\dfrac{\left(x+4\right)\left(x-3\right)}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x+4}{x^2+3x+9}\)
Để D=0 thi x+4=0
=>x=-4
\(E=\dfrac{2x\left(x^2+2x+1\right)}{2x\left(x-2\right)}=\dfrac{\left(x+1\right)^2}{x-2}\)
Để E=0 thì (x+1)^2=0
=>x=-1
TN
7
MH
29 tháng 3 2022
a) \(\text{Δ}=8^2-4.3.4=16\)
\(\left[{}\begin{matrix}x=\dfrac{-8+4}{2.3}=-\dfrac{2}{3}\\x=\dfrac{-8-4}{2.3}=-2\end{matrix}\right.\)
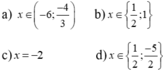
\(x^2\left(2x+3\right)-8x-12=0\)
\(\Rightarrow x^2\left(2x+3\right)-4\left(2x+3\right)=0\)
\(\Rightarrow\left(x^2-4\right)\left(2x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2-4=0\\2x+3=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=2\\x=-2\\x=-\frac{3}{2}\end{cases}}\)
\(x^2\left(2x+3\right)-8x-12=0\)
\(\Leftrightarrow\)\(x^2\left(2x+3\right)-4\left(2x+3\right)=0\)
\(\Leftrightarrow\)\(\left(2x+3\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\)\(\left(2x+3\right)\left(x-2\right)\left(x+2\right)=0\)
lm tiếp nhé