tìm trên mặt phẳng tọa độ Oxy, tọa độ của điểm M(x; y) phải thỏa mãn điều kiện gì để hoành độ bằng 2?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


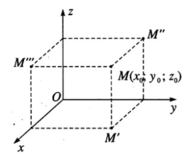
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )

\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)

Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .

\(b,\) PT hoành độ giao điểm: \(-2x+5=x+2\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow M\left(1;3\right)\)

Thay x=0 vào y=x+2013, ta được:
y=0+2013=2013
Thay y=0 vào y=x+2013, ta được:
x+2013=0
hay x=-2013

Cách 1:
Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)
Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)
\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)
\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)
\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)
Dấu "=" xảy ra khi và chỉ khi:
\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)
\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Cách 2:
Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)
Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:
\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)
Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)
\(\Rightarrow C\left(2;2\right)\)
Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)
Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)
\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD
\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)

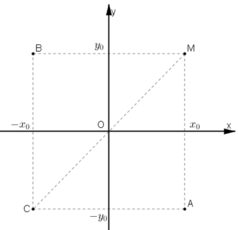
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).

a: Khi x=0 thì y=4
Khi y=0 thì -2x+4=0
hay x=2
b: Gọi điểm cần tìm là A(x;x)
Thay y=x vào y=-2x+4, ta được:
x=-2x+4
=>x=4
Vậy: Điểm cần tìm là A(4;4)
trên mặt phẳng tọa độ Oxy, tọa độ của điểm M(x; y) phải thỏa mãn điều kiện gì để hoành độ bằng 2?
Trả lời:
x=2
mk ko chắc lắm