Cho hcn ABCD, kẻ AH vuông góc với đường chéo BD.
a. Chứng minh BC2=DH.DB.
b. Gọi S là trung điểm của BH, R là trung điểm của AH. Chứng minh SH.BD=SR.DC.
c.Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hành.
d. Tính số đo góc AST.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 1 2019
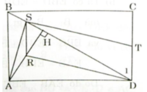
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
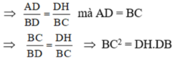
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
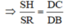
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o
17 tháng 3 2023
a: Xet ΔAHD vuông tại H và ΔDCB vuông tại C có
góc ADH=góc DBC
=>ΔAHD đồng dạng vơi ΔDCB
c: Xét ΔHAB có HN/HA=HM/HB
nên MN//AB
=>MN vuông góc AD
mà AH vuông góc DM
và AH cắt MN tại N
nên N là trực tâm
=>ND vuông góc AM
=>ME vuông góc AM
27 tháng 10 2021
a: Xét ΔHAB có
N là trung điểm của HB
M là trung điểm của HA
Do đó: NM là đường trung bình của ΔAHB
Suy ra: \(NM=\dfrac{AB}{2}=2\left(cm\right)\)
4 tháng 7 2022
a: Xét ΔABD vuông tại A có AH là đường cao
nên \(AD^2=DH\cdot DB=BC^2\)
c: Xét ΔHAB có
R là trung điểm của HA
S là trung điểm của HB
Do đó: RS là đường trung bình
=>RS//AB và RS=AB/2
=>RS//DT và RS=DT
=>RSTD là hình bình hành
21 tháng 10 2021
a: Xét tứ giác MFCE có
\(\widehat{MFC}=\widehat{MEC}=\widehat{FCE}=90^0\)
Do đó: MFCE là hình bình hành
Suy ra: MC=EF