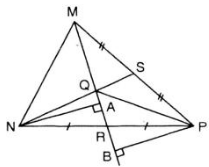
Hãy sử dụng tỉ số diện tích hai tam giác để chứng minh định lí về tính chất đường phân giác của tam giác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vẽ PB ⊥ MR
Vậy tam giác MPQ và RPQ có chung đường cao PB
Vì Q là trọng tâm của ΔMNR nên MQ = 2QR
Ta có :
\(S\Delta MPQ=\frac{1}{2}MQ.PB=\frac{1}{2}.2QR.PB=QR.PB\)
\(S\Delta RPQ=\frac{1}{2}QR.PB\)
Vậy \(\frac{S\Delta MPQ}{S\Delta RPQ}=\frac{QR.PB}{\frac{1}{2}QR.PB}=2\)
b) Vẽ NA ⊥ MR
Vậy NA là đường cao của ΔMNQ đồng thời là đường cao của ΔRNQ.
Vì Q là trọng tâm của ΔMNP nên MQ = 2QR
Ta có :
\(S\Delta MNQ=\frac{1}{2}MQ.NA=\frac{1}{2}.2QR.NA=QR.NA\)
\(S\Delta RNQ=\frac{1}{2}QR.NA\)
Vậy \(\frac{S\Delta MNQ}{S\Delta RNQ}=\frac{QR.NA}{\frac{1}{2}QR.NA}=2\)
c) \(\Delta NRA=\Delta PRB\) => NA=PB
Ta có :\(S\Delta RPQ=\frac{1}{2}QR.PB=\frac{1}{2}QR.NA=S\Delta RNQ\)
Vậy SΔRPQ = SΔRNQ
- Từ kết quả câu a) ta có:
SΔQPM = 2SΔPRQ = SΔQNP (do câu c) (*)
- Từ kết quả câu b) ta có:
SΔQMN = 2SΔRNQ = SΔQNP (**)
Từ (*) và (**) suy ra:
SΔQMN = SΔQNP = SΔQPM (đpcm)

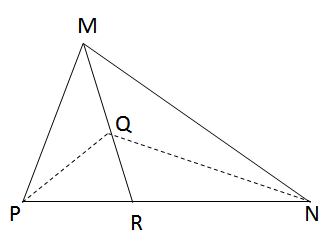
a) Vì Q là trọng tâm của ∆MNP nên điểm Q thuộc đường trung tuyến MR và MQRQ=2MQRQ=2.
Vì hai tam giác ∆MPQ và ∆RPQ có chung đường cao kẻ từ P nên :
SΔMPQSΔRPQ=MQRQ=2SΔMPQSΔRPQ=MQRQ=2 (1)
b) Chứng minh tương tự như câu (a) ta có :
SΔMPQSΔRPQ=2(2)SΔMPQSΔRPQ=2(2)
c) Hai tam giác ∆PQR và ∆QNR có chung đường cao kẻ từ Q và PR = RN nên S∆PQR = S∆QNR
Vì S∆PQR + S∆QNR = S∆PQN
Nên S∆PQN = 2.S∆PQR = 2.S∆QNR (3)
Từ (1), (2), (3) => S∆QMN = S∆QNP = S∆QPM

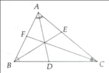
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA đồng dạng với ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=400\)
=>\(BC=\sqrt{400}=20\left(cm\right)\)
c: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{3}{4}\)
=>\(S_{ABD}=\dfrac{3}{4}\cdot S_{ACD}\)
d: Ta có: \(\dfrac{BD}{CD}=\dfrac{3}{4}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
mà BD+CD=BC=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
=>\(BD=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);CD=\dfrac{20}{7}\cdot4=\dfrac{80}{7}\left(cm\right)\)
e: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>AH=192/20=9,6(cm)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
c: AD là phân giác
=>BD/CD=AB/AC=3/4
=>S ABD/S ACD=3/4
d: BD/CD=3/4
=>BD/3=CD/4
mà BD+CD=10
nên BD/3=CD/4=10/7
=>BD=30/7cm; CD=40/7cm