x2-\(\sqrt{x^2-5}\)=7
giải dùm mình đc ko? Mình cần gấp lắm. Xin cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vd1:
d) Ta có: \(\sqrt{2}\left(x-1\right)-\sqrt{50}=0\)
\(\Leftrightarrow\sqrt{2}\left(x-1-5\right)=0\)
\(\Leftrightarrow x=6\)

Ta có : (x - 1)5 - 1 = 36
=> (x - 1)5 = 37
=> (x - 1) + 5 ko thỏa mãn
mình sửa lại đề nha: (x-1)5 - 1 = 36
Mình xin lỗi mn nhìu lắm

Bài 2
b, `\sqrt{3x^2}=x+2` ĐKXĐ : `x>=0`
`=>(\sqrt{3x^2})^2=(x+2)^2`
`=>3x^2=x^2+4x+4`
`=>3x^2-x^2-4x-4=0`
`=>2x^2-4x-4=0`
`=>x^2-2x-2=0`
`=>(x^2-2x+1)-3=0`
`=>(x-1)^2=3`
`=>(x-1)^2=(\pm \sqrt{3})^2`
`=>` $\left[\begin{matrix} x-1=\sqrt{3}\\ x-1=-\sqrt{3}\end{matrix}\right.$
`=>` $\left[\begin{matrix} x=1+\sqrt{3}\\ x=1-\sqrt{3}\end{matrix}\right.$
Vậy `S={1+\sqrt{3};1-\sqrt{3}}`

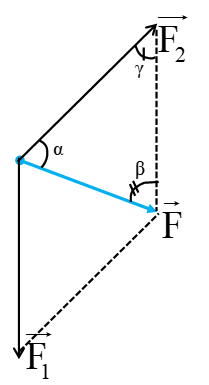
Theo định lí \(sin\):
\(\dfrac{sin\alpha}{F_1}=\dfrac{sin\beta}{F_2}=\dfrac{sin\gamma}{F}\)\(\Rightarrow F_2=\dfrac{F_1}{sin\alpha}\cdot sin\beta\)
\(F_{min}\Leftrightarrow sin\alpha=1\Rightarrow\alpha=90^o\)
\(\Rightarrow\beta=120-90=60^o\)
\(\Rightarrow F_2=\dfrac{6}{1}\cdot sin60^o=3\sqrt{3}N\)

Coi điểm tựa G là trung điểm AB.
Ta có hệ:
\(\left\{{}\begin{matrix}AH+HB=L=80\\3AH=HB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AH=20\\BH=60\end{matrix}\right.\)
\(\Rightarrow HG=\dfrac{1}{4}AB=\dfrac{1}{4}\cdot80=20cm\)
\(\Rightarrow GB=BH-HG=60-20=40cm\)

\(x^2-\sqrt{x^2-5}=7\)
\(\Leftrightarrow\sqrt{x^2-5}=x^2-7\)
\(\Leftrightarrow\left(\sqrt{x^2-5}\right)^2=\left(x^2-7\right)^2\)
\(\Leftrightarrow x^2-5=\left(x^2\right)^2-2.x^2.7+7^2\)
\(\Leftrightarrow x^2-5=x^4-14x^2+49\)
\(\Leftrightarrow-x^4+x^2+14x^2-5-49=0\)
\(\Leftrightarrow-x^4+15x^2-54=0\)
Đặt : \(t=x^2\left(t\ge0\right)\) , ta có :
\(-t^2+15t-54=0\)
\(\left(a=-1;b=15;c=-54\right)\)
\(\Delta=b^2-4ac\)
\(=15^2-4.\left(-1\right).\left(-54\right)\)
\(=225+4.\left(-54\right)\)
\(=225-216\)
\(=9>0\)
\(\sqrt{\Delta}=\sqrt{9}=3\)
\(t_1=\frac{-15+3}{2.\left(-1\right)}=6\) ( nhận )
\(t_2=\frac{-15-3}{2.\left(-1\right)}=9\) ( nhận )
Vs : \(t_1=6\Rightarrow x^2=6\Rightarrow x=\pm\sqrt{6}\)
Vs : \(t_2=9\Rightarrow x^2=9\Rightarrow x=\pm3\)
Vậy phương trình có 4 nghiệm : \(x_1=3;x_2=-3;x_3=6;x_4=-6\)
Cái đề có gì đó sai sai
\(\)