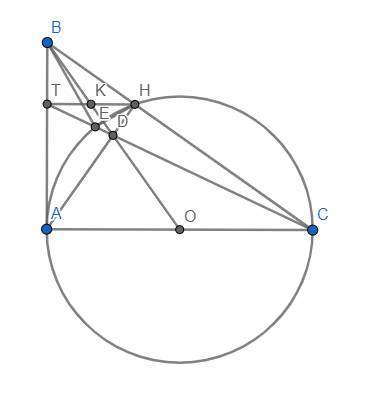
Cho đường tròn tâm O đường kính AB=2R. Cho C là điểm chính giữa của cung AB. Trên đoạn AB lấy điểm E sao cho BE=AC. Vẽ EH vuông góc với AC tại H. Tia phân giác của góc BAC cắt EH tại đường tròn tại điểm thứ hai là D. Tia AC và BD cắt nhau tại M. Tia CK cắt AB tại I và cắt đường tròn tại điểm thứ hai là F.
1) Tính so đo góc AMB
2) Chứng minh EH song song với BC
3) Chứng minh AFEK nội tiếp
4) Chứng minh I là trung điểm của AE
5)AD cắt CE tại I. Chứng minh CI đi qua trung điểm của HJ
6)Vẽ đường kính CP, CB cắt AD tại O', MO' cắt AB tại N. Chứng minh P,N,D thẳng hàng
7)AD cắt CO tại S, BS cắt AC tại Q. Chứng minh QC.QM=QS.QB
8)Chứng minh PNCE là hình thoi và góc NPE = 45o, CN là phân giác của OCP
9)CD cắt AB tại L. Chứng minh LN.LO=LP.LA và NB.AL=NA.BL
10)CN cắt AD tại V. Chứng minh VL,DN,CB đồng quy