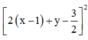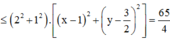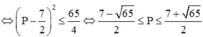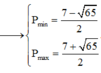xé các số x,y thỏa mãn x2 +y2=1. ìm giá trị lớn nhất của biểu thức P=2x+y3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Ta có P = 2 x 3 + y 3 - 3 x y = 2 x + y x 2 - x y + y 2 - 3 x y = 2 x + y 2 - x y - 3 x y
Mặt khác x 2 + y 2 = 2 ⇔ x + y 2 - 2 x y = 2 ⇔ 2 x y = x + y 2 - 2 ≤ x + y 2 2 ⇔ - 2 ≤ x + y ≤ 2
Khi đó 2 P = 2 x + y 4 - 2 x y - 6 x y = 2 x + y 4 - x + y 2 + 2 - 3 x + y 2 - 2
= 6 + 12 x + y - 3 x + y 2 - 2 x + y 3 = f t = 6 + 12 t - 3 t 2 - 2 t 3
Với t = x + y ∈ - 2 ; 2
Xét hàm số f t = 6 + 12 t - 3 t 2 - 2 t 3 trên đoạn [-2;2] ta có
f ' t = 12 - 6 t - 6 t 2 ; f ' t = 0 ⇔ [ t = - 2 t = 1
So sánh các giá trị f(-2);f(1);f(2), ta được m a x - 2 ; 2 f t = f 1 = 13 ⇒ M = 13 2 .

Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3

Đáp án C.
Phương pháp giải: Dựa vào giả thiết, đánh giá đưa về tổng các bình phương, từ biểu thức P đưa về hạng tử trong tổng bình phương và áp dụng bất đẳng thức Bunhiacopxki tìm giá trị lớn nhất.
Lời giải:
Vì x2 + y2 > 1 suy ra log x 2 + y 2 f ( x ) là hàm số đồng biến trên tập xác định
Khi đó ![]()
![]()
![]()
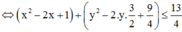
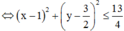
Xét biểu thức P, ta có 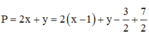
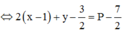
Áp dụng BĐT Bunhiacopxki, có