Cho hình chữ nhật ABCD.Lấy điểm K nằm trong hình chữ nhật sao cho K cách AB 1cm và cách AC 8cm. Qua K kẻ một đương thẳng cắt cả AB và AC ở M và N (N nằm giữa A và B,M nằm giữa A và C). Tính chiều dài ngắn nhất của MN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


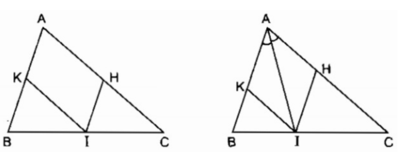
Hình bình hành AHIK là hình chữ nhật
⇒ ∠ A = 90 0 suy ra ∆ ABC vuông tại A. Ngược lại ΔABC có ∠ A = 90 0
Suy ra hình bình hành AHIK là hình chữ nhật
Vậy nếu ∆ ABC vuông tại A thì tứ giác AHIK là hình chữ nhật.

a: góc AKB=1/2*180=90 độ
góc AKE+góc AHE=180 độ
=>AKEH nội tiếp
b: XétΔCKM và ΔCNA có
góc CKM=góc CNA
góc C chung
=>ΔCKM đồng dạng với ΔCNA
=>CK/CN=CM/CA
=>CN*CM=CK*CA
XétΔCKE vuông tại K và ΔCHA vuông tại H có
góc HCA chung
=>ΔCKE đồng dạng với ΔCHA
=>CK/CH=CE/CA
=>CK*CA=CH*CE=CN*CM

a) Xét tứ giác MNCP có
MN // CP(gt)
MP // NC(gt)
\(\Rightarrow\)Tứ giác MNCP là hình bình hành
b) Xét hình bình hành MNCP là hình thoi
\(\Leftrightarrow\)MN=MP
\(\Leftrightarrow\)Tam giác AMN= Tam giác MBP
Xét tam giác AMN và tam giác MBP có
\(\widehat{AMN}\)= \(\widehat{MBP}\)
\(\widehat{BMP}\)= \(\widehat{MAN}\)
Vậy để Tam giác AMN= Tam giác MBP
\(\Leftrightarrow\)AM=MB
Vậy khi M là trung điểm của AB thì MNCP là Hình thoi
c) Hình bình hành MNCP là Hình chữ nhật
\(\Leftrightarrow\)\(\widehat{C}\)=90 độ
\(\Leftrightarrow\)Tam giác ABC vuông tại C
Vậy khi Tam giác ABC vuông tại C thì MNCP là Hình chữ nhật
