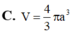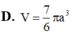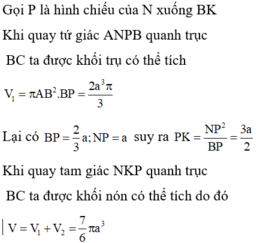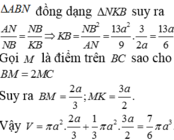Cho S là hình vuông với cạnh là 100, và L là đường gấp khúc không tự cắt tạo thành từ các đoạn thẳng A0A1, A1A2…,An-1An với A0#An. Giả sử với mỗi điểm P trên biên của S đều có một điểm thuộc L cách P không quá ½. Hãy chứng minh: Tồn tại 2 điểm X và Y thuộc L sao cho khoảng cách giữa X và Y không vượt qúa 1, và độ dài phần đường gấp khúc L nằm giữa X và Y không nhỏ hơn 198.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh SA1, SA2,.... SAn, tương ứng tại B1, B2,..., Bn nên theo định lý Talet trong từng tam giác SA1A2, …, SAn-1An thì \(\frac{{S{B_1}}}{{S{A_1}}} = \frac{{S{B_2}}}{{S{A_2}}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = ... = \frac{{S{B_n}}}{{S{A_n}}}\) mà S.A1A2...An là hình chóp đều nên S.B1B2...Bn cũng là một hình chóp đều.
b) Ta có \(SH \bot \left( {{A_1}{A_2}...{A_n}} \right)\) (H là tâm của đa giác A1A2...An)
Mà \(\left( {{A_1}{A_2}...{A_n}} \right)//\left( {{B_1}{B_2}...{B_n}} \right)\)
\( \Rightarrow \)\(SH \bot \left( {{B_1}{B_2}...{B_n}} \right)\)
Mà \(SK \bot \left( {{B_1}{B_2}...{B_n}} \right)\) (K là tâm của đa giác B1B2...Bn)
\( \Rightarrow \) SH trùng SK
Vậy đường thẳng SH đi qua tâm K của đa giác đều B1B2...Bn, và HK vuông góc với các mặt phẳng (A1A2...An), (B1B2...Bn)

Đáp án D
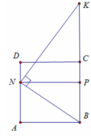
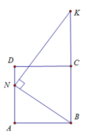
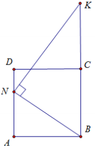
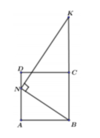
Gọi P là hình chiếu của N xuống BK
Khi quay tứ giác ANPB quanh trục BC ta được khối trụ có thể tích V 1 = πAB 2 . BP = 2 a 3 π 3
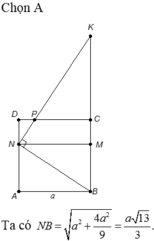
Lại có B P = 2 3 a ; N P = a suy ra P K = N P 2 B P = 3 a 2
Khi quay tam giác NKP quanh trục BC ta được khối nón có thể tích do đó V = V 1 + V 2 = 7 6 πa 3

Phương pháp:
Công thức tính thể tích của khối trụ có bán kính đáy R và chiều cao h: V = π R 2 h
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h: V = 1 3 π R 2 h
Cách giải:
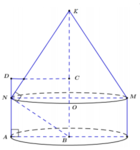
Khi quay tứ giác ANKB quanh trục BK ta được hình trụ có bán kính đáy AB, chiều cao AN và hình nón có bán kính đáy AB, chiều cao K O = B K − A N
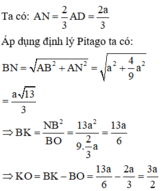
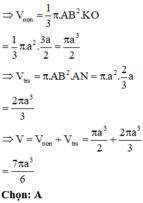

a: ΔHEB vuông tại H có góc HBE=45 độ
nên ΔHEB vuông cân tại H
b: KH//AB
=>gó KHE=góc HEB=45 độ
=>ΔKHM vuôngtại K
=>KH=KM
ΔCKH vuông tại K có góc C=45 độ
nên ΔCKH vuông cân tại K
=>KC=KH=KM
=>K là trung điểm của MC