Cho ba số x;y;z khác 0 thoả mãn:
\(\frac{xy}{2y+3x}\)= \(\frac{yz}{5y+3z}\)= \(\frac{xz}{2z+5x}\)
Chứng minh x;y;z tỉ lệ với 2;3;5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 10 2017
Đáp án C
Theo giả thiết ta có: x + 2 y = 10 2 x y = 16 ⇒ y = 8 x x + 16 x = 10 ⇒ 2 y = 16 x x 2 - 10 x + 16 = 0 ⇔ [ x = 8 x = 2 2 y = 16 x
⇒ [ x = 8 2 y = 2 x = 2 2 y = 8 ⇒ x - 2 y = 6 .
CM
25 tháng 2 2019
Chọn C.
Theo tính chất của cấp số cộng và cấp số nhân ta có
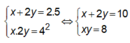
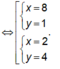
Vậy |x-2y| = 6
NT
0
22 tháng 9 2023
\(-\) Do \(c^x\) nghịch biến\(,a^x,b^x\) đồng biến\(\Rightarrow c< 1,a>1,b>1\Rightarrow c\) nhỏ nhất \(\Rightarrow\)Loại \(C,D\)
\(-\) Dựa vào đồ thị ta thấy\(,b^x\) có đồ thị đi lên cao hơn so với \(a^x\Rightarrow b>a\Rightarrow\) Chọn \(A\)
TH
1
