Cho \(\Delta ABC\) góc A= 90o, AB<AC. Vẽ AH\(\perp\)BC tại H, vẽ HI \(\perp\)AB tại I. Trên tia HI lấy D sao cho I là trung điểm của DH
a) C/m \(\Delta ADI=\Delta AHI\)
b) AD\(\perp\)BD
c) Cho BH = 9cm, HC = 10cm. Tính AH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
QN
2
TL
Trịnh Long
CTVVIP
26 tháng 6 2021
Xét tam giác ABH và ACH
=> 2 tam giác trên đồng dạng
=> \(\dfrac{AH}{HC}=\dfrac{AB}{AC}\)
\(mà\dfrac{AB}{AC}=\dfrac{5}{7}=>\dfrac{AH}{HC}=\dfrac{5}{7}=>HC=\dfrac{7.15}{5}=21\left(cm\right)\)
Áp dụng hệ thức lượng :
AH^2 = HB.HC => HB = \(\dfrac{15^2}{21}=\dfrac{75}{7}\left(cm\right)\)
26 tháng 6 2021
*Đề bài viết thiếu đường cao AH :v
Xét tam giác AHB và tam giác CHA có:
góc AHB = góc CHA = 90o
góc BAH = góc C ( cùng phụ với góc B)
⇒\(\dfrac{AH}{HC}=\dfrac{AB}{AC}=\dfrac{HB}{AH}\)
Theo đề bài ta có : \(\dfrac{AB}{AC}=\dfrac{5}{7}\)
⇒\(\dfrac{AB}{AC}=\dfrac{HB}{AH}\Leftrightarrow\dfrac{5}{7}=\dfrac{HB}{15}\Leftrightarrow HB=\dfrac{75}{7}\left(cm\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AH}{HC}\Leftrightarrow\dfrac{5}{7}=\dfrac{15}{HC}\Leftrightarrow HC=21\left(cm\right)\)
PT
1
CM
8 tháng 6 2017
- Cách vẽ:
+ Vẽ góc xAy = 90o
+ Trên tia Ax vẽ đoạn thẳng AB = 3cm
+ Trên tia Ay vẽ đoạn thẳng AC = 3cm
+ Vẽ đoạn thẳng BC
Ta được tam giác ABC là tam giác cần vẽ
- Đo các góc B và C ta được góc B = góc C = 45º
CM
23 tháng 6 2019
a) + Δ ABC vuông tại A, có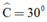 
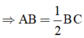
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của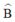 
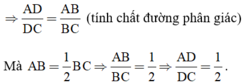
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
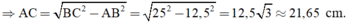
+ Chu vi tam giác ABC là:
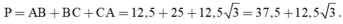
+ Diện tích tam giác ABC là:
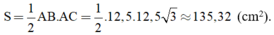
Hình ảnh bạn tự vẽ nhé!
a/ Tam giác ADI vuông tại I và tam giác ADI vuông tại I có:
ID = IH ( vì I là trung điểm của HD)
IA là cạnh chung
=> \(\Delta ADI=\Delta AHI\)( hai cạnh góc vuông)
b/ Tam giác ADB và tam giác AHB có:
AD = AH ( tam giác ADI = tam giác AHI)
\(\widehat{DAI}\) = \(\widehat{HAI}\)( vì tam giác ADI = tam giác AHI)
BA là cạnh chung.
=> Tam giác ADB = tam giác AHB ( c.g.c)
=> D = H = 90 độ
=> AD\(\perp\)BD tại D