Cho tam giác ABC có \(\widehat{B}-\widehat{C}=90\) độ. Kẻ các đường phân giác trong AD và phân giác ngoài AE. (D,E thuộc đường thẳng BC). C/minh: AD = AE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
25 tháng 5 2019
a, Do DE//BC
=> \(\widehat{A_1}=\widehat{ABC}\)( so le trong )
Vì \(\widehat{BAz}\)là góc ngoài tam giác ABC
=> \(\widehat{BAz}=\widehat{ABC}+\widehat{ACB}\)
\(\Rightarrow\widehat{A_1}+\widehat{A_2}=\widehat{ABC}+\widehat{ACB}\)
Do \(\widehat{A_1}=\widehat{ABC}\)( chứng minh trên )
\(\Rightarrow\widehat{A_2}=\widehat{ACB}\)
Mà góc ABC = góc ACB ( tam giác ABC cân ở A )
=> \(\widehat{A_1}=\widehat{A_2}\)
=> Ax là tia phân giác góc BAz
Hay Ax là phân giác góc ngoài đỉnh A của tam giác ABC
b, Vì \(\widehat{A_2}=\widehat{CAE}\)( 2 góc đối đỉnh)
Mà \(\widehat{A_2}=\widehat{A_1}\)(cmt)
\(\Rightarrow\widehat{A_1}=\widehat{CAE}\)
\(\Rightarrow\widehat{A_1}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}\)
\(\Rightarrow\widehat{DAC}=\widehat{EAB}\)
Vì góc ABC = góc ACB ( tam giác ABC cân )
=> \(\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\Rightarrow\widehat{ABE}=\widehat{ACD}\)
Xét tam giác DAC và tam giác EAB có:
\(\widehat{ACD}=\widehat{ABE}\)( chứng minh trên )
AC = AB ( tam giác ABC cân )
\(\widehat{DAC}=\widehat{EAB}\)( chứng minh trên )
=> \(\Delta DAC=\Delta EAB\)( g-c-g )
=> DA = EA
A
19 tháng 6 2019
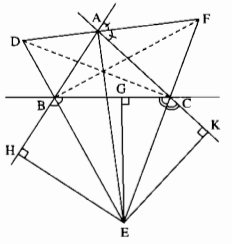
a) E thuộc tia phân giác của \(\widehat{CBH}\)
\(\Rightarrow\)EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của \(\widehat{BCK}\)
\(\Rightarrow\)EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
\(\Rightarrow\)E thuộc tia phân giác của \(\widehat{BAC}\)mà E khác A
Vậy AE là tia phân giác của \(\widehat{BAC}\)
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
\(\Rightarrow AE\perp AF\) (tính chất hai góc kề bù)
Hay \(AE\perp DF\)
d) Chứng minh tương tự câu a ta có BF là tia phân giác của \(\widehat{ABC}\)
CD là tia phân giác của \(\widehat{ACB}\)
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
\(\Rightarrow BF\perp BE\) (tính chất hai góc kề bù)
Hay \(BF\perp ED\)
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
\(\Rightarrow CD\perp CE\)(tính chất hai góc kề bù)
Hay \(CD\perp EF\)
Các đường thẳng AE, FB, DC là các đường cao trong tam giác DEF.
