Question

[Kim Khánh Linh]

Bài 2 (trang 45 SGK Toán 9 Tập 1)

Cho hàm số $y=-\dfrac{1}{2} x+3$.

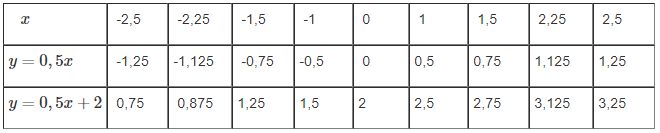
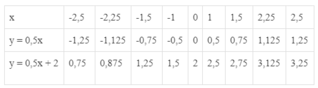
a) Tính các giá trị tương ứng của y theo các giá trị của $x$ rồi điền vào bảng sau :

$x$	$-2,5$	$-2$	$-1,5$	$-1$	$-0,5$	$0$	$0,5$	$1$	$1,5$	$2$	$2,5$
$y=-\dfrac{1}{2} x+3$

b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?

Answer 1

[Phạm Hoàng Khánh Chi]

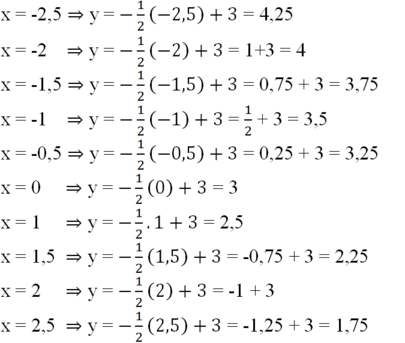
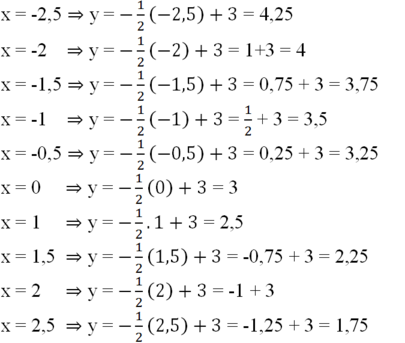
a) Ta có y=f(x)=−1/2x+3y=f(x)=−1/2x+3.

Với y=−1/2x+3y=−1/2x+3 thay các giá trị của xx vào biểu thức của yy, ta được:

+) f(−2,5)=−1/2.(−2,5)+3f(−2,5)=−1/2.(−2,5)+3

=(−0,5).(−2,5)+3=(−0,5).(−2,5)+3=1,25+3=4,25=1,25+3=4,25

+)  f(−2)=−1/2.(−2)+3f(−2)=−1/2.(−2)+3

 =(−0,5).(−2)+3=1+3=4=(−0,5).(−2)+3=1+3=4.

 +) f(−1,5)=−1/2.(−1,5)+3f(−1,5)=−1/2.(−1,5)+3

=(−0,5).(−1,5)+3=(−0,5).(−1,5)+3=0,75+3=3,75=0,75+3=3,75.

 +) f(−1)=−1/2.(−1)+3f(−1)=−1/2.(−1)+3

=(−0,5).(−1)+3=0,5+3=3,5=(−0,5).(−1)+3=0,5+3=3,5.

+) f(−0,5)=−1/2.(−0,5)+3f(−0,5)=−1/2.(−0,5)+3

=(−0,5).(−0,5)+3=(−0,5).(−0,5)+3=0,25+3=3,25=0,25+3=3,25.

 +) f(0)=−1/2.0+3f(0)=−1/2.0+3=(−0,5).0+3=0+3=3=(−0,5).0+3=0+3=3

 +) f(0,5)=−1/2.0,5+3f(0,5)=−1/2.0,5+3

=(−0,5).0,5+3=(−0,5).0,5+3=−0,25+3=2,75=−0,25+3=2,75

 +) f(1)=−1/2.1+3f(1)=−1/2.1+3

=(−0,5).1+3=−0,5+3=2,5=(−0,5).1+3=−0,5+3=2,5.

+) f(1,5)=−1/2.1,5+3f(1,5)=−1/2.1,5+3

=(−0,5).1,5+3=−0,75+3=(−0,5).1,5+3=−0,75+3=2,25=2,25

+)  f(2)=−1/2.2+3f(2)=−1/2.2+3

=(−0,5).2+3=−1+3=2=(−0,5).2+3=−1+3=2.

 +) f(2,5)=−1/2.2,5+3f(2,5)=−1/2.2,5+3

=(−0,5).2,5+3=−1,25+3=(−0,5).2,5+3=−1,25+3=1,75=1,75

Ta có bảng sau:

b)

Nhìn vào bảng giá trị của hàm số ở câu a ta thấy khi xx càng tăng thì giá trị của f(x)f(x) càng giảm. Do đó hàm số nghịch biến trên R

Answer 2

[Đỗ Văn Công]

a)

$x$	$-2,5$	$-2$	$-1,5$	$-1$	$-0,5$	$0$	$0,5$	$1$	$1,5$	$2$	$2,5$
y=-\dfrac{1}{2} x+3	$4,25$	$4$	$3,75$	$3,5$	$3,25$	$3$	$2,75$	$2,5$	$2,25$	$2$	$1,75$

b) Khi $x$ lần lượt nhận các giá trị tăng lên thì giá trị tương ứng của hàm số lại giảm đi. Vậy hàm số đã cho nghịch biến trên $\mathbb{R}$.