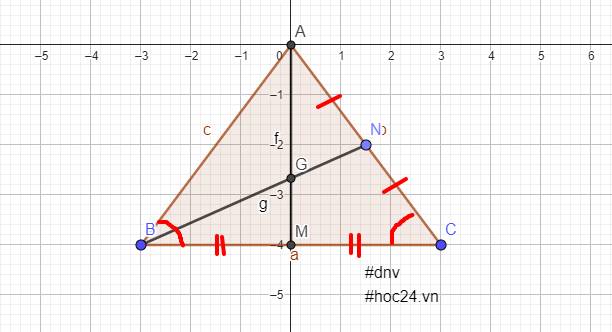
Cho tam giác ABC cân tại A, trung tuyến AM, BN của tam giác ABC cắt tại G.
a/ C.m Tam giác ABM= tam giác ACM
b/ C.m AM là tia phân giác góc BAC
c/ Trên tia đối của tia NG lấy điểm E sao cho NG=NE. C.m AE // CG
d/ C.m GM+GN>AB/2
Giải hộ câu d mình với
Cần gấp
Cảm ơn nhiều